《2025年课时训练江苏人民出版社八年级数学上册苏科版》

11 (2024·常州模拟)点 A(5,3)经过某种图形变化后得到点 B(-3,5),这种图形变化可能是(C).
A.关于 x 轴对称
B.关于 y 轴对称
C.绕原点逆时针旋转 90°
D.绕原点顺时针旋转 90°

答案： C

12 (2024·宜宾一模)若点 A(3,a)与 B(b,-2)关于原点对称,则点 M(a,b)在第四象限.

答案： 四

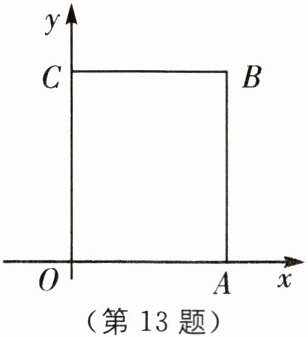
13 如图,在长方形 OABC 中,O 为平面直角坐标系的原点,点 A 的坐标为(a,0),点 C 的坐标为(0,b),且 a,b 满足√(a-4)+|b-6|= 0,点 B 在第一象限内,点 P 从原点出发,以每秒 2 个单位长度的速度沿着 O→A→B→C→O 的线路移动.
(1)求点 B 的坐标；
(2)当点 P 移动 4 秒时,请求出点 P 的坐标；
(3)当点 P 移动到距离 x 轴 5 个单位长度时,求点 P 移动的时间.

答案：
(1)
∵a,b满足√(a - 4)+|b - 6|=0,
∴a - 4 = 0,b - 6 = 0,解得a = 4,b = 6,
∴点A的坐标为(4,0),点C的坐标为(0,6),
∴OA = 4,OC = 6,
∴AB = 6,BC = 4,
∴点B的坐标是(4,6).
(2)
∵点P从原点出发,以每秒2个单位长度的速度沿着O→A→B→C→O的线路移动,
∴点P移动4秒时所走的路程为2×4 = 8.
∵OA = 4,OC = 6,
∴当点P移动4秒时,点P在线段AB上,且AP = 8 - 4 = 4,
即当点P移动4秒时,点P的坐标是(4,4).
(3)由题意可得,在移动过程中,当点P到x轴的距离为5个单位长度时,存在两种情况:
①当点P在AB上时,
点P移动的时间为(5 + 4)÷2 = 4.5(秒);
②当点P在OC上时,
点P移动的时间为[2×(4 + 6)-5]÷2 = 7.5(秒).
故在移动过程中,当点P到距离x轴5个单位长度时,点P移动的时间是4.5秒或7.5秒.

14 中考新考法 新定义问题 (2025·宿迁沭阳怀文中学期末)在平面直角坐标系中,对于任意两点$ P_1(x_1,y_1)$与$ P_2(x_2,y_2)$的“识别距离”,给出如下定义：
若|$x_1-x_2$|＞|$y_1-y_2$|,则点$ P_1(x_1,y_1)$与点$ P_2(x_2,y_2)$的“识别距离”为|$x_1-x_2$|；
若|$x_1-x_2$|＜|$y_1-y_2$|,则点$ P_1(x_1,y_1)$与点$ P_2(x_2,y_2)$的“识别距离”为|$y_1-y_2$|.
例如：对于点$ P_1(2,-1)$与点$ P_2(4,3),$因为|2-4|＜|-1-3|,所以点$ P_1$与点$ P_2$的“识别距离”为 4.
[初步理解]
(1)已知点 A(-1,0),B(1,3),则点 A 与点 B 的“识别距离”为______3.
[深入应用]
(2)已知点 A(2,0),点 B 为 y 轴上的一个动点.
①若点 A 与点 B 的“识别距离”为 4,求出满足条件的点 B 的坐标；
②点 A 与点 B 的“识别距离”的最小值为______2.
[知识迁移]
(3)已知点 C(m,2m-1),D(0,0),直接写出点 C 与点 D“识别距离”的最小值及对应的点 C 坐标.点C与D的“识别距离”的最小值1/3,相应的C点坐标为(1/3,-1/3).

答案：
(1)3
(2)①
∵B为y轴上的动点,
∴可设点B坐标为(0,b).
∵点A(2,0)与点B的“识别距离”为4,|2 - 0| = 2,
∴|0 - b| = 4,
∴b = ±4,
∴点B的坐标为(0,4)或(0,-4).
②2
(3)点C与D的“识别距离”的最小值1/3,相应的C点坐标为(1/3,-1/3).理由如下:
由“识别距离”的定义可知,点C与点D“识别距离”最小,|x₁ - x₂| = |y₁ - y₂|.
∵C(m,2m - 1),D(0,0),
∴|m - 0| = |m|,|2m - 1 - 0| = |2m - 1|,
∴|m| = |2m - 1|,解得m = 1或m = 1/3.
当m = 1时,“识别距离”为|1 - 0| = 1;
当m = 1/3时,“识别距离”为|1/3 - 0| = 1/3,
∴点C与点D的“识别距离”的最小值为1/3,相应的点C坐标为(1/3,-1/3).