第61页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
1 教材 P70探究·变式 (2025·扬州广陵区期末)下列各数中,是无理数的是(
A.$\frac{1}{3}$
B.3.14
C.$\frac{\pi}{2}$
D.0
C
).A.$\frac{1}{3}$
B.3.14
C.$\frac{\pi}{2}$
D.0
答案:
C
2 关于无理数的表述,错误的是(
A.无限不循环小数叫作无理数
B.无理数不能写成$\frac{m}{n}$($m,n$是整数,$n≠0$)的形式
C.无理数可以用数轴上的点表示
D.无理数就是指$\pi$和像 0.1010010001…这样的数
D
).A.无限不循环小数叫作无理数
B.无理数不能写成$\frac{m}{n}$($m,n$是整数,$n≠0$)的形式
C.无理数可以用数轴上的点表示
D.无理数就是指$\pi$和像 0.1010010001…这样的数
答案:
D
3 (2025·广东深圳月考改编)在实数$-\sqrt{5},3.14,0,\frac{\pi}{2},\frac{22}{7},-\sqrt{9},0.1616616661…$(两个1之间依次多一个6)中,无理数的个数是(
A.5
B.4
C.3
D.2
C
).A.5
B.4
C.3
D.2
答案:
C
4 下列说法正确的是(
A.有理数和无理数统称为实数
B.实数是由正实数和负实数组成
C.整数和分数统称为实数
D.有理数和数轴上的点一一对应
A
).A.有理数和无理数统称为实数
B.实数是由正实数和负实数组成
C.整数和分数统称为实数
D.有理数和数轴上的点一一对应
答案:
A
5 (2024·山东临沂期末)若将三个数$-\sqrt{3},\sqrt{7},\sqrt{10}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是(
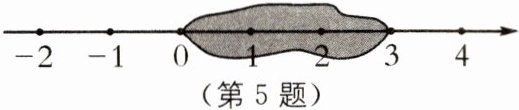
A.$-\sqrt{3}$
B.$\sqrt{7}和\sqrt{10}$
C.$\sqrt{10}$
D.$\sqrt{7}$
D
).
A.$-\sqrt{3}$
B.$\sqrt{7}和\sqrt{10}$
C.$\sqrt{10}$
D.$\sqrt{7}$
答案:
D
下列数中:6,$-3.14,\frac{8}{11},0,-\frac{\pi}{2},0.\dot{5}\dot{1},-\frac{7}{4},1.909009000…$(每两个9之间依次多一个0)中,是整数的有
6,0
;是负分数的有$-3.14$,$-\dfrac{7}{4}$
;是无理数的有$-\dfrac{\pi}{2}$,1.909009000…(每两个9之间依次多一个0)
.
答案:
6,0;$-3.14$,$-\dfrac{7}{4}$;$-\dfrac{\pi}{2}$,1.909009000…(每两个9之间依次多一个0)
7 教材 P72问题·改编(2025·福建三明三元区期中)如图,正方形$ABCD$的面积为7,顶点$A$在数轴上表示的数为1,若点$E$在数轴上(点$E在点A$的左侧),且$AD= AE$,则点$E$所表示的数为(
A.$\sqrt{7}$
B.$\sqrt{7}+1$
C.$-\sqrt{7}$
D.$1-\sqrt{7}$
D
).A.$\sqrt{7}$
B.$\sqrt{7}+1$
C.$-\sqrt{7}$
D.$1-\sqrt{7}$
答案:
D
8 (2024·无锡锡山区期中)有理数$a,b,c$在数轴上的位置如图所示.
(1)用“>”或“<”填空:$c-b$
(2)化简:$|c-b|+2|a+b|-|a-c|$.

(1)用“>”或“<”填空:$c-b$
>
0,$a+b$<
0,$a-c$<
0;(2)化简:$|c-b|+2|a+b|-|a-c|$.

$-a-3b$
答案:
(1)> < < [解析]
∵$a<0<b<c$,$|a|>|b|$,
∴$c-b>0$,$a+b<0$,$a-c<0$.
(2)
∵$c-b>0$,$a+b<0$,$a-c<0$,
∴$|c-b|+2|a+b|-|a-c|$$=c-b-2(a+b)+(a-c)$$=c-b-2a-2b+a-c=-a-3b$.
(1)> < < [解析]
∵$a<0<b<c$,$|a|>|b|$,
∴$c-b>0$,$a+b<0$,$a-c<0$.
(2)
∵$c-b>0$,$a+b<0$,$a-c<0$,
∴$|c-b|+2|a+b|-|a-c|$$=c-b-2(a+b)+(a-c)$$=c-b-2a-2b+a-c=-a-3b$.
9 (2024·北京二中期中)如图,点$A$是硬币圆周上一点,点$A$与数轴上2所对应的数重合.假设硬币的直径为1个单位长度,若将硬币按如图所示的方向滚动(无滑动)一周,点$A恰好与数轴上点A'$重合.则点$A'$对应的实数是(
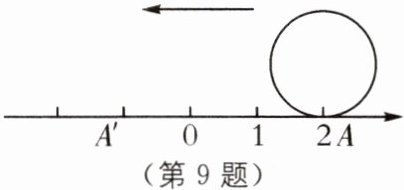
A.$2-2\pi$
B.$2+2\pi$
C.$2-\pi$
D.$2+\pi$
C
).
A.$2-2\pi$
B.$2+2\pi$
C.$2-\pi$
D.$2+\pi$
答案:
C
查看更多完整答案,请扫码查看


