第9页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图,在△ABC中,∠BAC= 90°,∠C= 30°,AD⊥BC,BE平分∠ABC交AD于点E,EF//AC交BC于点F,下列结论不成立的是 (
A.∠ABD= ∠DAC
B.∠C= ∠BAD
C.AC= 2AD
D.AD= 2DF
D
)A.∠ABD= ∠DAC
B.∠C= ∠BAD
C.AC= 2AD
D.AD= 2DF
答案:
D
2. 如图,在△ABC中,AC= 8,点D,E分别在边BC,AC上,F是BD的中点.若AB= AD,EF= EC,则EF的长是(
A.3
B.4
C.5
D.6
B
)A.3
B.4
C.5
D.6
答案:
B 提示:连接AF.因为AB=AD,F是BD 的中点,所以AF⊥BD,所以∠AFD=90°,所以∠EAF+∠C=90°,∠AFE+∠EFC=90°.因为EF=EC,所以∠EFC=∠C.所以∠EAF=∠AFE,所以EA=EF,所以EF=EA=EC=$\frac{1}{2}$AC=4.
3. 如图,已知∠MON= 30°,点$A_1,A_2,A_3,…$在射线ON上,点$B_1,B_2,B_3,…$在射线OM上$,△A_1B_1A_2,△A_2B_2A_3,△A_3B_3A_4,…$均为等边三角形.若$OA_1= 2,$则$△A_6B_6A_7$的边长为 (
A.16
B.32
C.64
D.128
C
)A.16
B.32
C.64
D.128
答案:
C 提示:因为△A₁B₁A₂为等边三角形,所以∠B₁A₁A₂=60°,A₁B₁=A₁A₂,所以∠A₁B₁O=∠B₁A₁A₂ - ∠MON=30°,所以∠A₁B₁O=∠MON,所以A₁B₁=OA₁,所以A₁B₁=A₁A₂=OA₁.同理可得A₂B₂=A₂A₃=OA₂=2OA₁,A₃B₃=A₃A₄=OA₃=2OA₂=2²·OA₁,A₄B₄=A₄A₅=OA₄=2OA₃=2³·OA₁,…,所以AₙBₙ=AₙAₙ₊₁=2ⁿ⁻¹·OA₁=2ⁿ,所以△A₆B₆A₇的边长A₆B₆=2⁶=64.
4. 如图,在△ABC中,∠C= 90°,∠A= 30°.若在BC或AC所在直线上取一点P,使△PAB是等腰三角形,则符合条件的点P有 (
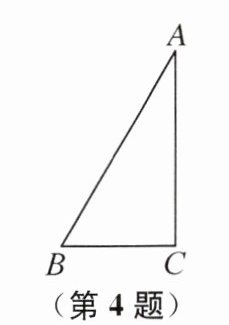
A.5个
B.6个
C.7个
D.8个
B
)
A.5个
B.6个
C.7个
D.8个
答案:
B 提示:如图,符合条件的点P有6个.
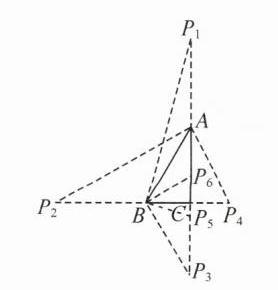
B 提示:如图,符合条件的点P有6个.

5. (2025天津市期末)如图,在△ABC中,AB= AC,BC= 4,S△ABC= 14,AC的垂直平分线EF分别交边AC,AB于点E,F.若D为边BC的中点,M为线段EF上的一个动点,则△CDM周长的最小值为 (
A.7
B.9
C.12
D.14
B
)A.7
B.9
C.12
D.14
答案:
B 提示:如图,连接AM,AD.因为AB=AC,BC=4,D为边BC的中点,所以CD=BD=$\frac{1}{2}$BC=2,AD⊥BC.因为$S_{\triangle ABC}=\frac{1}{2}×4AD=14$,所以AD=7.因为EF垂直平分AC,M为线段EF上的动点,所以AM=CM.因为AM+DM≥AD,所以CM+DM≥7,所以CM+DM+CD≥9,所以△CDM周长的最小值为9.
6. 如图,在边长为5的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB.将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M的运动过程中,线段HN长的最小值是 (
A.5/4
B.1
C.2
D.5/2
A
)A.5/4
B.1
C.2
D.5/2
答案:
A 提示:取BC的中点G,连接MG.易证△MBG≌△NBH,所以GM=HN.根据垂线段最短得,当MG⊥CH时,GM的长最短,即HN的长最短,此时∠BCH=30°,CG=$\frac{1}{2}$BC=$\frac{5}{2}$,所以MG=$\frac{1}{2}$CG=$\frac{5}{4}$,所以HN长的最小值是$\frac{5}{4}$.
7. 若等腰三角形两腰上的高所在直线的夹角是70°,则它的顶角的度数是______
110°或70°
.
答案:
110°或70° 提示:分2种情况讨论:如图1,当∠BAC是钝角时,根据题意,得AB=AC,∠AEH=∠ADH=90°,∠EHD=70°,所以∠BAC=∠EAD=360° - 90° - 90° - 70°=110°;如图2,当∠A是锐角时,根据题意,得AB=AC,∠CDA=∠BEA=90°,∠CHE=70°,所以∠DHE=110°,所以∠A=360° - 90° - 90° - 110°=70°.综上所述,该等腰三角形的顶角的度数为110°或70°.
8. 如图,在以AB为斜边的两个Rt△ABC和Rt△ABD中,∠ACB= ∠ADB= 90°,CD= m,AB= 2m,则∠AEB=
120°
.
答案:
120° 提示:如图,取AB的中点F,连接CF,DF.因为∠ACB=∠ADB=90°,所以CF=$\frac{1}{2}$AB=DF.又因为CD=m,AB=2m,所以CD=$\frac{1}{2}$AB,所以CF=DF=CD,所以△CDF是等边三角形,所以∠CFD=60°,所以∠AFC+∠BFD=120°.因为CF=BF,AF=DF,所以∠1=∠2,∠3=∠4.因为∠AFC=∠1+∠2,∠BFD=∠3+∠4,所以∠2+∠3=$\frac{1}{2}$∠AFC+$\frac{1}{2}$∠BFD=$\frac{1}{2}$(∠AFC+∠BFD)=60°,所以∠AEB=180° - (∠2+∠3)=120°.
9. 如图,在△ABC中,∠ACB= 90°,AC= BC= 4,D是边BC的中点,P是边AC上一个动点,连接PD,以PD为边在PD的下方作等边三角形PDQ,连接CQ.则CQ长的最小值是______
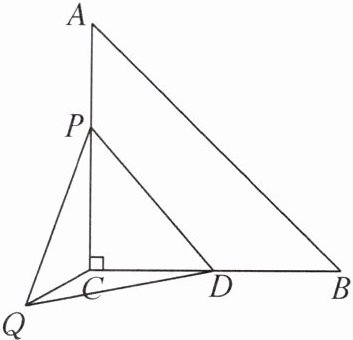
1
.
答案:
1 提示:如图,在CD的下方作等边三角形CDT.因为∠CDP=60° - ∠CDQ=∠TDQ,PD=QD,CD=TD,所以△CDP≌△TDQ(SAS),所以∠DTQ=∠DCP=90°.因为∠CTD=60°,所以∠CTQ=30°,所以点Q在射线TG上运动(T是定点,∠CTQ是定角),当CQ⊥TQ时,CQ的值最小,最小值为CH的长,且CH=$\frac{1}{2}$CT=$\frac{1}{2}$CD=$\frac{1}{4}$BC=1.
查看更多完整答案,请扫码查看


