第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
9. 周长为30,各边互不相等且都是整数的三角形共有
12
个.
答案:
12 提示:设三角形三边为a,b,c,且a<b<c.因为a+b+c=30,a+b>c,所以10<c<15.因为c为整数,所以c的值可以为11,12,13,14.①当c=14时,有5个三角形,三边长分别是14,13,3;14,12,4;14,11,5;14,10,6;14,9,7.②当c=13时,有4个三角形,三边长分别是13,12,5;13,11,6;13,10,7;13,9,8.③当c=12时,有2个三角形,三边长分别是12,11,7;12,10,8.④当c=11时,有1个三角形,三边长分别是11,10,9.
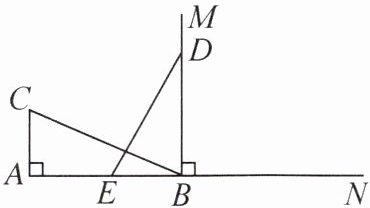
10. 如图,CA⊥AB,垂足为A,AB= 24cm,AC= 12cm,射线BM⊥AB,垂足为B.一动点E从点A出发以3cm/s的速度沿射线AN匀速运动,D为射线BM上一动点,随着点E运动而运动,且始终保持ED= CB,求经过多少秒时,以D,E,B为顶点的三角形与以B,C,A为顶点的三角形全等.

答案:
解:设经过ts时,以D,E,B为顶点的三角形与以B,C,A为顶点的三角形全等,则AE=3tcm.根据题意,分2种情况讨论.当点E 在点B的左侧时,若△DEB≌△BCA,则BE=AC,即24−3t=12,解得t=4;若△DEB≌△CBA,则BE=AB,即24−3t=24,解得t=0.当点E在点B的右侧时,若△DEB≌△BCA,则BE=AC,即3t−24=12,解得t=12;若△DEB≌△CBA,则BE=AB,即3t−24=24,解得t=16.综上所述,当点E经过0s或4s或12s或16s时,以D,E,B为顶点的三角形与以B,C,A为顶点的三角形全等.
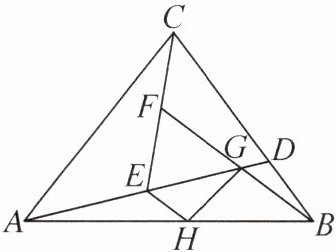
11. 如图,在△ABC中,D是边BC上一点,BD∶CD= 1∶2,连接AD,E是线段AD的中点,连接CE,F是线段CE的中点,连接BF交线段AD于点G,过点E作EH//BF交AB于点H,连接HG.给出下列结论:①S△ACE= S△DCE;②S△BCF= 1/4S△ABC;③S△EFG= S△GBH;④S△EFG+S△DBG= S四边形CFGD.其中正确的个数是(
A.1
B.2
C.3
D.4
C
)
A.1
B.2
C.3
D.4
答案:
C 提示:连接BE,DF,设S△ABD=2S,则S△ACD=4S,S△ABC=6S.因为E是线段AD的中点,所以S△ACE=S△DCE=2S,故①正确;可知S△BCE=S△DCE+S△DBE=3S,因为F是线段CE的中点,所以S△BCF=1/2S△BCE=3/2S,所以S△BCF:S△ABC=1:4,即S△BCF=1/4S△ABC,故②正确;易得S△DEF=S△DBE,设点F到DE的距离为m,点B到DE的距离为n,所以1/2DE·m=1/2DE·n,则m=n,因为S△DFG=1/2DG·m,S△DBG=1/2DG·n,所以S△DFG=S△DBG,所以S△DEF−S△DFG=S△DBE−S△DBG,即S△EFG=S△EBG=1/2S△BEF=3/4S,因为EH//BF,所以S△GBH=S△EBG=S△EFG,故③正确;因为S△EFG+S△DBG=S△EBG+S△DBG=S,四边形CFGD=S△DCE−S△EFG=5/4S,所以S△EFG+S△DBG≠S四边形CFGD,故④错误.
12. 【操作与实践】
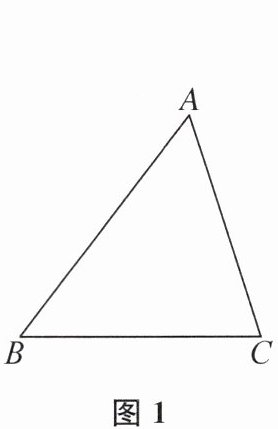
(1)如图1,请你在△ABC中画一条线段,把△ABC分成面积相等的两部分.
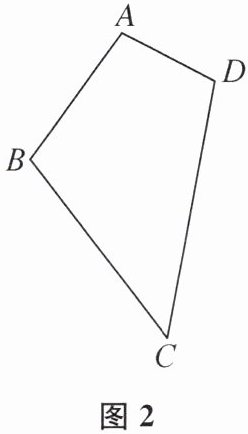
(2)如图2,请你按照(1)的方法把四边形ABCD分成面积相等的两部分.
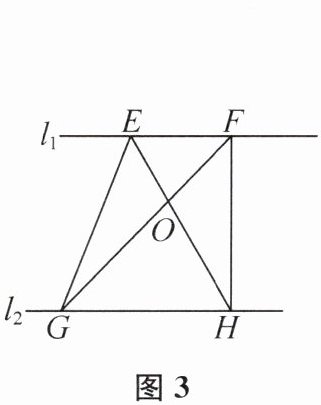
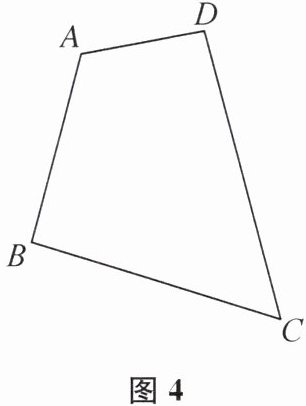
(3)如图3,已知$l_1//l_2,$点E,F在$l_1$上,点G,H在$l_2$上,则△EGO与△FHO的面积相等;利用以上性质尝试在如图4所示的四边形ABCD中作一条线段,把四边形ABCD分成面积相等的两部分,请简要写出画图步骤.
(1)如图1,请你在△ABC中画一条线段,把△ABC分成面积相等的两部分.
(2)如图2,请你按照(1)的方法把四边形ABCD分成面积相等的两部分.
(3)如图3,已知$l_1//l_2,$点E,F在$l_1$上,点G,H在$l_2$上,则△EGO与△FHO的面积相等;利用以上性质尝试在如图4所示的四边形ABCD中作一条线段,把四边形ABCD分成面积相等的两部分,请简要写出画图步骤.




答案:
解:
(1)如图1,线段AD即为所求.

(2)如图2所示,即为所求. 提示:易知S△ADE=S△CDE,S△ABE=S△BCE,所以S△ADE+S△ABE=S△CDE+S△BCE,所以S四边形ABED=S四边形BCDE.

(3)如图3,连接AC,BD,取AC的中点O,过点O作OE//BD交CD于点E,连接BE,则线段BE把四边形ABCD分成面积相等的两部分. 提示:连接OD交BE于点F,连接OB.因为OE//BD,所以S△DEF=S△OBF.因为O是AC的中点,所以S△ADO=S△CDO,S△ABO=S△CBO,所以S△BCE=S△CBO+S△OBF+S△CBO+S△OEF=S△CBO+S△DEF+S△CBO+S△OEF=S△CBO+S△CDO,S四边形ABED=S四边形ABFD+S△DEF=S△ABO+S△ADO−S△OBF+S△DEF=S△ABO+S△ADO=S△CBO+S△CDO.所以S△BCE=S四边形ABED.所以线段BE把四边形ABCD分成面积相等的两部分.

解:
(1)如图1,线段AD即为所求.

(2)如图2所示,即为所求. 提示:易知S△ADE=S△CDE,S△ABE=S△BCE,所以S△ADE+S△ABE=S△CDE+S△BCE,所以S四边形ABED=S四边形BCDE.

(3)如图3,连接AC,BD,取AC的中点O,过点O作OE//BD交CD于点E,连接BE,则线段BE把四边形ABCD分成面积相等的两部分. 提示:连接OD交BE于点F,连接OB.因为OE//BD,所以S△DEF=S△OBF.因为O是AC的中点,所以S△ADO=S△CDO,S△ABO=S△CBO,所以S△BCE=S△CBO+S△OBF+S△CBO+S△OEF=S△CBO+S△DEF+S△CBO+S△OEF=S△CBO+S△CDO,S四边形ABED=S四边形ABFD+S△DEF=S△ABO+S△ADO−S△OBF+S△DEF=S△ABO+S△ADO=S△CBO+S△CDO.所以S△BCE=S四边形ABED.所以线段BE把四边形ABCD分成面积相等的两部分.

查看更多完整答案,请扫码查看


