《2025年小题狂做八年级数学上册苏科版巅峰版》

15. 如图1,这是由8个同样大小的正方体组成的魔方,体积为8.

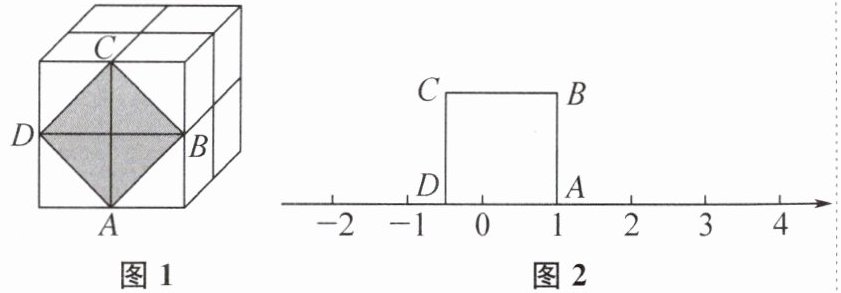
(1) 图1中的阴影部分是一个正方形ABCD,则它的面积为2,边长为$\sqrt{2}$.
(2) 如图2把正方形ABCD放到数轴上,使得点A与1对应的点重合,那么点D在数轴上表示的数为$1-\sqrt{2}$.
(3) 在(2)的条件下,把正方形ABCD沿数轴逆时针方向滚动.当点B第一次落在数轴上时,求点B在数轴上表示的数.
解:当点B第一次落在数轴上时,正方形向左滚动了两次,相当于点A向左移动了$3AD=3\sqrt{2}$的长度,又因为点A与1对应的点重合,所以点B在数轴上表示的数为$1-3\sqrt{2}$.

答案：
(1)2 $\sqrt{2}$
(2)$1-\sqrt{2}$
(3)解:当点B第一次落在数轴上时,正方形向左滚动了两次,相当于点A向左移动了$3AD=3\sqrt{2}$的长度,又因为点A与1对应的点重合,所以点B在数轴上表示的数为$1-3\sqrt{2}$.

16. 在做某物理实验时,小华用一根细线将一正方体铁块拴住,完全浸入盛满水的圆柱形烧杯中,并用一量筒量得被铁块排出的水的体积为$64\ \text{cm}^3$,小华又将铁块从烧杯中提起,量得烧杯中的水位下降了3 cm.请问烧杯内部的底面圆的半径和铁块的棱长各是多少($\pi$取3,结果保留整数)?

答案： 解:设正方体铁块的棱长是x cm.根据题意,得$x^{3}=64$,解得$x=4$.所以正方体铁块的棱长是4 cm.
设烧杯内部的底面圆半径是r cm.根据题意,得$\pi r^{2}×3=64$.因为$\pi$取3,所以$r^{2}=\frac{64}{9}$.因为$r＞0$,所以$r=\frac{8}{3}\approx3$.所以烧杯内部的底面圆的半径约是3 cm.

(1) 求110592的立方根,写出步骤.
解:第一步:因为$\sqrt[3]{1000}=10$,$\sqrt[3]{1000000}=100$,$1000＜110592＜1000000$,所以$10＜\sqrt[3]{110592}＜100$,所以能确定110592的立方根是个两位数.第二步:因为110592的个位数是2,$8^{3}=512$,所以能确定110592的立方根的个位数是8.第三步:如果划去110592后面的三位592得到数110,而$\sqrt[3]{64}＜\sqrt[3]{110}＜\sqrt[3]{125}$,则$4＜\sqrt[3]{110}＜5$,可得$40＜\sqrt[3]{110592}＜50$,由此能确定110592的立方根的十位数是4,因此110592的立方根是48.
(2) 填空:$\sqrt[3]{85184}= $44.

答案：
(1)解:第一步:因为$\sqrt[3]{1000}=10$,$\sqrt[3]{1000000}=100$,$1000＜110592＜1000000$,所以$10＜\sqrt[3]{110592}＜100$,所以能确定110592的立方根是个两位数.第二步:因为110592的个位数是2,$8^{3}=512$,所以能确定110592的立方根的个位数是8.第三步:如果划去110592后面的三位592得到数110,而$\sqrt[3]{64}＜\sqrt[3]{110}＜\sqrt[3]{125}$,则$4＜\sqrt[3]{110}＜5$,可得$40＜\sqrt[3]{110592}＜50$,由此能确定110592的立方根的十位数是4,因此110592的立方根是48.
(2)44 提示:同理能确定85184的立方根是个两位数.因为85184的个位数是4,$4^{3}=64$,所以能确定85184的立方根的个位数是4.而$\sqrt[3]{64}＜\sqrt[3]{85}＜\sqrt[3]{125}$,则$4＜\sqrt[3]{85}＜5$,可得$40＜\sqrt[3]{85184}＜50$,由此能确定85184的立方根的十位数是4,因此85184的立方根是44.

18. 已知实数a,b,c,d满足$2022a^3= 2023b^3= 2024c^3= 2025d^3$,$\sqrt[3]{2022a^2+2023b^2+2024c^2+2025d^2}= \sqrt[3]{2022}+\sqrt[3]{2023}+\sqrt[3]{2024}+\sqrt[3]{2025}$,求$a^{-1}+b^{-1}+c^{-1}+d^{-1}$的值.

答案： 解:由题意知,a,b,c,d均不为0.设$2022a^{3}=2023b^{3}=2024c^{3}=2025d^{3}=k(k\neq0)$,则$2022a^{2}=\frac{k}{a}$,$2023b^{2}=\frac{k}{b}$,$2024c^{2}=\frac{k}{c}$,$2025d^{2}=\frac{k}{d}$,$\frac{k}{a^{3}}=2022$,$\frac{k}{b^{3}}=2023$,$\frac{k}{c^{3}}=2024$,$\frac{k}{d^{3}}=2025$.所以$\sqrt[3]{\frac{k}{a}+\frac{k}{b}+\frac{k}{c}+\frac{k}{d}}=\sqrt[3]{\frac{k}{a^{3}}}+\sqrt[3]{\frac{k}{b^{3}}}+\sqrt[3]{\frac{k}{c^{3}}}+\sqrt[3]{\frac{k}{d^{3}}}$,所以$\sqrt[3]{k(a^{-1}+b^{-1}+c^{-1}+d^{-1})}=\sqrt[3]{k}(a^{-1}+b^{-1}+c^{-1}+d^{-1})$,所以$\sqrt[3]{k}\sqrt[3]{a^{-1}+b^{-1}+c^{-1}+d^{-1}}=\sqrt[3]{k}(a^{-1}+b^{-1}+c^{-1}+d^{-1})$,所以$\sqrt[3]{a^{-1}+b^{-1}+c^{-1}+d^{-1}}=a^{-1}+b^{-1}+c^{-1}+d^{-1}$,又因为$2022a^{3}=2023b^{3}=2024c^{3}=2025d^{3}$,所以a,b,c,d为同号,所以$a^{-1}+b^{-1}+c^{-1}+d^{-1}=\pm1$.