第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图,在Rt△ABC中,∠ACB= 90°,AC= 6,BC= 8,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD延长线上的点B'处,两条折痕与斜边AB分别交于点E,F,则线段B'F的长为(
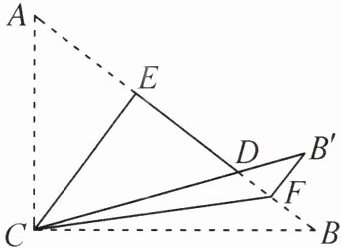
A.$\frac{6}{5}$
B.$\frac{8}{5}$
C.$\frac{4}{3}$
D.$\sqrt{3}$
B
)
A.$\frac{6}{5}$
B.$\frac{8}{5}$
C.$\frac{4}{3}$
D.$\sqrt{3}$
答案:
B 提示:根据勾股定理,得AB=√(AC²+BC²)=10.根据折叠的性质,可得CE⊥AB,B'F=BF,∠ACE=∠DCE,∠BCF=∠B'CF.所以∠ECF=1/2∠ACB=45°,所以△ECF是等腰直角三角形.用等积法可求得CE=EF=24/5.根据勾股定理,得AE=18/5,所以B'F=BF=AB - AE - EF=8/5.
2. 若P是等边三角形ABC内一点,$PA^{2}+PB^{2}= PC^{2}$,且PC= 2PA,则∠BPC的度数为( )
A.75°
B.90°
C.120°
D.135°
A.75°
B.90°
C.120°
D.135°
答案:
B 提示:如图,将△ABP绕点B顺时针旋转60°,使BA与BC重合,BP移至BM处,PA移至MC处,所以BM=BP,MC=PA,∠PBM=60°.连接MP,则△BPM是等边三角形,所以PB=PM.因为PA²+PB²=PC²,所以MC²+PM²=PC²,所以△PMC是直角三角形,∠CMP=90°.因为PC=2PA,所以PC=2MC.取PC的中点G,连接MG,易证∠CPM=30°.又因为∠BPM=60°,所以∠BPC=90°.

B 提示:如图,将△ABP绕点B顺时针旋转60°,使BA与BC重合,BP移至BM处,PA移至MC处,所以BM=BP,MC=PA,∠PBM=60°.连接MP,则△BPM是等边三角形,所以PB=PM.因为PA²+PB²=PC²,所以MC²+PM²=PC²,所以△PMC是直角三角形,∠CMP=90°.因为PC=2PA,所以PC=2MC.取PC的中点G,连接MG,易证∠CPM=30°.又因为∠BPM=60°,所以∠BPC=90°.

3. 如图,已知直线a//b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB的长度是面积为120的正方形边长的长度.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的值最小,则此时AM+NB等于( )
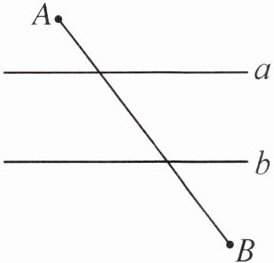
A.6
B.8
C.10
D.12

A.6
B.8
C.10
D.12
答案:
B 提示:如图,作M'N'⊥a,分别交a,b于点M',N',连接AM'并沿M'N'方向平移至A'N',连接A'B交直线b于点N,过点N作NM⊥a于点M,则此时的M,N即为所要找的点.连接AM,易证△AMM'≌△A'NN',则A'N=AM,AM'=A'N'.易知AA'=M'N'=4.所以AM+NB=A'N+NB=A'B(连接N'B,则AM'+N'B=A'N'+N'B≥A'B,当点N'与点N重合时取等号).过点B作BE⊥AA',交AA'的延长线于点E,易得AE=2 + 4 + 3=9,A'E=5.在Rt△AEB中,BE²=AB² - AE²=39.在Rt△A'EB中,A'B²=A'E²+BE²,解得A'B=8.

B 提示:如图,作M'N'⊥a,分别交a,b于点M',N',连接AM'并沿M'N'方向平移至A'N',连接A'B交直线b于点N,过点N作NM⊥a于点M,则此时的M,N即为所要找的点.连接AM,易证△AMM'≌△A'NN',则A'N=AM,AM'=A'N'.易知AA'=M'N'=4.所以AM+NB=A'N+NB=A'B(连接N'B,则AM'+N'B=A'N'+N'B≥A'B,当点N'与点N重合时取等号).过点B作BE⊥AA',交AA'的延长线于点E,易得AE=2 + 4 + 3=9,A'E=5.在Rt△AEB中,BE²=AB² - AE²=39.在Rt△A'EB中,A'B²=A'E²+BE²,解得A'B=8.

4. 如图,若AB= 5,AC= 3,边BC上的中线AD= 2,则△ABC的面积为
6
.
答案:
6 提示:延长AD至点E,使ED=AD,连接BE.因为D为BC的中点,所以DC=DB.在△ADC和△EDB中,{AD = ED,∠ADC = ∠EDB,DC = DB},所以△ADC≌△EDB.所以EB=AC=3.又因为AE=2AD=4,AB=5,所以AB²=AE²+EB²,所以∠E=90°.所以S△ABC=S△ABD+S△ADC=S△ABD+S△EDB=S△ABE=6.
5. 如图,E是正方形ABCD内的一点,连接AE,BE,CE,将△ABE绕点B顺时针旋转90°到△CBE'的位置.若AE= 1,BE= 2,CE= 3,则∠BE'C= ______.


135°
答案:
135° 提示:连接EE'.根据旋转的性质,得∠EBE'=90°,BE'=BE=2,CE'=AE=1.所以△BEE'是等腰直角三角形,所以∠BE'E=45°.由勾股定理,得EE'²=8.因为EE'²+CE'²=CE²,所以∠EE'C=90°.所以∠BE'C=∠BE'E+∠EE'C=135°.
6. 如图,在△ABC中,∠ACB= 90°,AC= 6,AB= 10,O是边AB的中点,P是射线AC上的一个动点,BQ//CA,交PO的延长线于点Q,OM⊥PQ交边BC于点M.当CP= 1时,BM的长为
2.5或1
.
答案:
2.5或1 提示:连接MQ,MP,设BM=x.由勾股定理,得BC=√(AB² - AC²)=8.当点P在线段AC上时,因为QB//AP,所以∠A=∠OBQ.易证△OAP≌△OBQ,所以QB=PA=5,OQ=OP.因为OM⊥PQ,所以MQ=MP,所以5²+x²=1²+(8 - x)²,解得x=2.5.当点P在AC的延长线上时,同理可得7²+x²=1²+(8 - x)²,解得x=1.综上所述,BM的长为2.5或1.
7. 在等腰三角形ABC中,AB= AC= 1,线段BC上有2025个不同的点$P_{1},P_{2},P_{3},…,P_{2025}$,记$m_{i}= AP_{i}^{2}+BP_{i}\cdot P_{i}C(i= 1,2,3,…,2025)$,则$m_{1}+m_{2}+m_{3}+… +m_{2025}= $
2025
.
答案:
2025 提示:过点A作AD⊥BC于点D.因为APᵢ²=AD²+PᵢD²=AD²+(BD - BPᵢ)²=AD²+BD² - 2BD·BPᵢ+BPᵢ²=1+BPᵢ(BPᵢ - BC)=1 - BPᵢ·PᵢC,所以mᵢ=APᵢ²+BPᵢ·PᵢC=1.所以m₁+m₂+…+m₂₀₂₅=2025.
查看更多完整答案,请扫码查看


