《2025年小题狂做八年级数学上册苏科版巅峰版》

1. 如图,△ABC 的面积等于 6,边 AC= 3.现将△ABC 沿 AB 所在直线翻折,使点 C 落在直线 AD 上的点 C'处,点 P 在直线 AD 上,则线段 BP 的长不可能是 (A)
A.3
B.4
C.5
D.6

答案： A 提示:过点B作BN⊥AC，交AC的延长线于点N,BM⊥AD于点M.由折叠的性质，得∠C'AB=∠CAB.由角平分线的性质，得BN=BM.因为△ABC的面积等于6,AC=3,所以BN=BM=4,所以BP≥4.

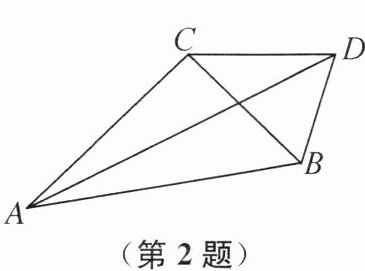
2. 如图,在四边形 ABDC 中,对角线 AD 平分∠BAC,∠ACD= 136°,∠BCD= 44°,则∠ADB 的度数为 ( )

A.54°
B.50°
C.48°
D.46°

答案：
D 提示:如图，过点D作DE⊥AB于点E,DF⊥AC于点F,DG⊥BC于点G.因为AD平分∠BAC,所以DF=DE.因为∠DCF=44°,∠BCD=44°,所以CD平分∠BCF,所以DF=DG.因为DE=DF=DG,所以BD平分∠CBE,所以∠ADB=∠DBE−∠BAD=$\frac{1}{2}$(∠CBE−∠BAC)=$\frac{1}{2}$∠ACB=$\frac{1}{2}$(∠ACD−∠BCD)=46°.

3. 如图,在△ABC 中,AD⊥BC 于点 D,AE 平分∠BAC 交 BC 于点 E,F 为 BC 的延长线上一点,FG⊥AE 交 AD 的延长线于点 G,AC 的延长线交 FG 于点 H,连接 BG,下列结论：① ∠DAE = ∠F；②2∠DAE= ∠ABD-∠ACE；③S△AEB：S△AEC= AB：AC；④∠AGH= ∠BAE＋∠ACB.其中正确的结论有 (D)
A.1个
B.2个
C.3个
D.4个

答案： D 提示:设AE交GF于点M.因为AD⊥BC,FG⊥AE,所以∠ADE=∠AMF=90°,因为∠AED=∠MEF,所以∠DAE=∠F,故①正确;因为AE平分∠BAC,所以∠EAC=$\frac{1}{2}$∠BAC，所以∠DAE=90°−∠AED=90°−(∠ACE+∠EAC)=90°−(∠ACE+$\frac{1}{2}$∠BAC)=$\frac{1}{2}$(180°−2∠ACE−∠BAC)=$\frac{1}{2}$(∠ABD−∠ACE),即2∠DAE=∠ABD−∠ACE,故②正确;又因为AE平分∠BAC,所以点E到AB和AC的距离相等,所以$S_{\triangle AEB}:S_{\triangle AEC}=AB:AC$,故③正确,因为∠DAE=∠F,∠FDG=∠FME=90°,所以∠AGH=∠MEF,因为∠MEF=∠CAE+∠ACB,所以∠AGH=∠CAE+∠ACB=∠BAE+∠ACB,故④正确

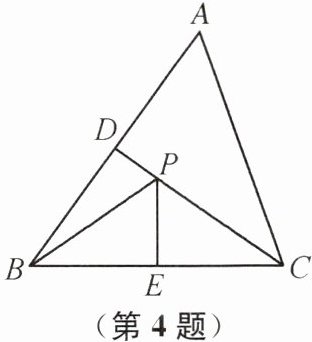
4. 如图,在△ABC 中,∠BAC= 56°,PD 垂直平分 AB,PE 垂直平分 BC,则∠BPC= ______°.

112

答案： 112 提示:连接PA.因为PD垂直平分AB，PE垂直平分BC,所以PA=PB=PC,所以∠PBA=∠PAB,∠PCA=∠PAC,所以∠PBA+∠PCA=∠PAB+∠PAC=∠BAC=56°.所以∠PBC+∠PCB=180°−∠A−(∠PBA+∠PCA)=68°,所以∠BPC=180°−(∠PBC+∠PCB)=112°.

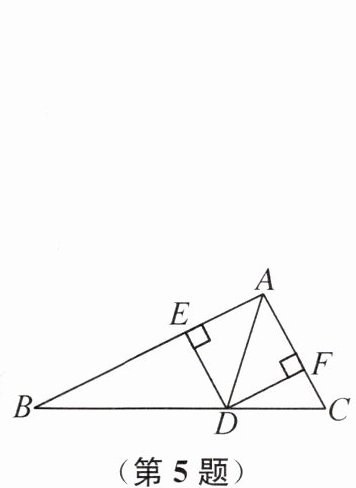
5. 如图,在△ABC 中,AD 是∠BAC 的平分线,DE⊥AB 于点 E,DF⊥AC 于点 F.若S△ABC= 9,DE= 2,AB= 6,则 AC 的长是______.

3

答案： 3 提示:因为AD是∠BAC的平分线,DE⊥AB,DF⊥AC,所以DF=DE=2.又因为$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ACD}=9$,AB=6,所以$\frac{1}{2}×6×2+\frac{1}{2}AC\cdot2=9$,所以AC=3.

6. 如图,P 是∠AOB 外的一点,M,N 分别是∠AOB 两边上的点,点 P 关于 OA 的对称点 Q 恰好落在线段 MN 上,点 P 关于 OB 的对称点 R 落在 MN 的延长线上.若PM= 3 cm,PN= 4 cm,MN= 5.5 cm,则线段 QR 的长为6.5cm.

答案： 6.5 提示:根据轴对称的性质，可知OA垂直平分PQ,OB垂直平分PR,所以QM=PM=3cm，RN=PN=4cm.因为MN=5.5cm,所以QN=MN−QM=2.5cm.所以QR=QN+RN=6.5cm.

7. 如图,在△ABC 中,AD 平分∠BAC,DG⊥BC 且平分 BC,DE⊥AB 于点 E,DF⊥AC,交 AC 的延长线于点 F.若AB= 5,AC= 3,则 AE 的长为______4.

答案： 4 提示:连接BD,CD.因为AD平分∠BAC,DE⊥AB,DF⊥AC,所以DE=DF,∠EAD=∠FAD,∠BED=∠CFD=90°.因为DG⊥BC且平分BC,所以BD=CD.在Rt△BED和Rt△CFD中,$\begin{cases} BD=CD \\ DE=DF \end{cases}$所以Rt△BED≌Rt△CFD,所以BE=CF.在△AED和△AFD中,$\begin{cases} \angle AED=\angle AFD \\ \angle EAD=\angle FAD \\ AD=AD \end{cases}$所以△AED≌△AFD,所以AE=AF.设BE=CF=x.因为AB=5,AC=3,所以5−x=3+x,解得x=1,即BE=1.所以AE=AB−BE=4.

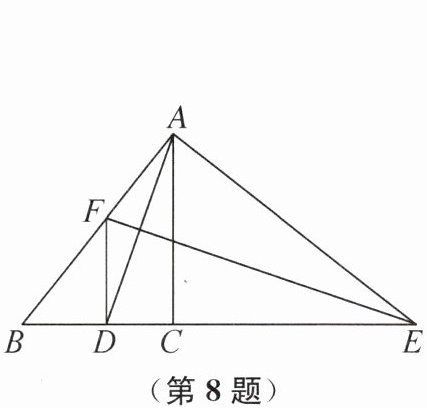
8. 如图,已知 AD 是△ABC 的角平分线,AD 的垂直平分线交 AB 于点 F,交 BC 的延长线于点 E. 以下四个结论：①∠EAD= ∠EDA；② DF // AC；③∠FDE= 90°；④∠B= ∠CAE.其中结论正确的是______(填序号).

①②④

答案： ①②④ 提示:因为EF是AD的垂直平分线,所以EA=ED,所以∠EAD=∠EDA,故①正确;因为EF是AD的垂直平分线，所以FA=FD,所以∠FDA=∠FAD,因为AD平分∠BAC,所以∠FAD=∠CAD,所以∠FDA=∠CAD,所以DF//AC,故②正确;因为FD与BE不一定互相垂直,所以③不一定正确;因为∠EDA=∠B+∠FAD,∠EAD=∠CAD+∠CAE,∠EAD=∠EDA,∠FAD=∠CAD,所以∠B=∠CAE,故④正确