第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
8. 如图,某地有两所大学和两条交叉的公路. 图中点M,N表示大学,OA,OB表示公路,现计划修建一座图书馆,希望图书馆到两所大学的距离相同,到两条公路的距离也相同,你能确定出图书馆P应该建在什么位置吗?请在图中画出你的设计(尺规作图,不写作法,保留作图痕迹).


答案:
解:如图所示,点$P_1$和点$P_2$即为所求.
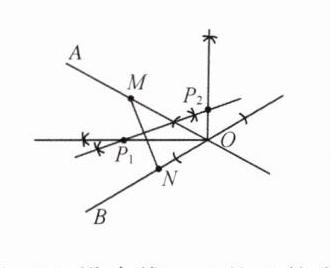
解:如图所示,点$P_1$和点$P_2$即为所求.

9. 如图,在平面直角坐标系xOy中,点A(0,3),B(-4,0),连接AB,C为线段AB上的一个动点(点C不与点A,B重合),过点C作CP⊥x轴,垂足为P. 将线段AP绕点A逆时针旋转至AQ,且∠PAQ= ∠BAO,连接OQ,设点C的横坐标为m.

(1)求直线AB的函数表达式.
(2)求当m为何值时,△ACP≌△AOQ.
(3)在点C的运动过程中,
①在y轴上是否存在一点D,使得∠ADQ的大小始终不发生变化?若存在,求出点D的坐标;若不存在,请说明理由.
②连接OQ,请直接写出OQ长的取值范围.


(1)求直线AB的函数表达式.
(2)求当m为何值时,△ACP≌△AOQ.
(3)在点C的运动过程中,
①在y轴上是否存在一点D,使得∠ADQ的大小始终不发生变化?若存在,求出点D的坐标;若不存在,请说明理由.
②连接OQ,请直接写出OQ长的取值范围.

答案:
解:
(1)设直线AB的函数表达式为$y = kx + b(k \neq 0)$.所以$\begin{cases}-4k + b = 0\\b = 3\end{cases}$,解得$\begin{cases}k = \frac{3}{4}\\b = 3\end{cases}$.所以直线AB的函数表达式为$y = \frac{3}{4}x + 3$.
(2)因为$\angle BAO = \angle PAQ$,所以$\angle BAO - \angle PAO = \angle PAQ - \angle PAO$,即$\angle BAP = \angle OAQ$.因为$AP = AQ$,所以当$AC = AO = 3$时,$\triangle ACP \cong \triangle AOQ$.因为点$C(m,\frac{3}{4}m + 3)$,所以$m^{2} + (3 - \frac{3}{4}m - 3)^{2} = 3^{2}$,解得$m = -\frac{12}{5}$或$m = \frac{12}{5}$(舍去).所以当m的值为$-\frac{12}{5}$时,$\triangle ACP \cong \triangle AOQ$.
(3)①存在.如图1,若点C与点B重合,则点P在点$P'$处,与点B重合,点Q在y轴上的点$Q'$处.由
(2)得,$\angle P'AP = \angle Q'AQ$.又因为$AP = AQ$,$AP' = AQ'$,所以$\triangle P'AP \cong \triangle Q'AQ$,所以$\angle AQ'Q = \angle AP'P = \angle ABP$为定角.所以点Q在以$Q'$为端点的射线上运动(不包括点$Q'$),所以在y轴上存在一点D,使得$\angle ADQ$的大小始终不发生变化,此时点D与点$Q'$重合.因为$AD = AP' = AB = \sqrt{OA^{2} + OB^{2}} = 5$,所以点$D(0, -2)$.
②$\frac{6}{5} \leq OQ < \sqrt{\frac{36}{5}}$. 提示:如图2,由①知,点Q在射线DV上运动(不包括点D).过点O作$OE \perp DV$于点E,当点Q运动到点E时,OQ的值最小,设DV交x轴于点H.因为$\angle ADV = \angle ABO$,所以$\angle DOE = \angle BCP$,所以$\angle AOE = \angle ACP$.因为$\angle CAP = \angle OAE$,$AP = AE$,所以$\triangle CAP \cong \triangle OAE$.所以$OA = CA = 3$,$OE = CP$.同
(2),得点$C(-\frac{12}{5},\frac{6}{5})$,所以$OE = CP = \frac{6}{5}$.如图3,当点C运动到点A时,点Q运动到点F,此时$\angle BAO = \angle FAO$,$AF \perp DV$,$OQ$的值最大.作点F关于y轴的对称点G,此时点G落在线段AB上,可得$AF = OA = AG = 3$,$OF = OG$.由
(2),得点$G(-\frac{12}{5},\frac{6}{5})$,所以$OF = OG = \sqrt{(-\frac{12}{5})^{2} + (\frac{6}{5})^{2}} = \sqrt{\frac{36}{5}}$.因为点C不与点A重合,所以$OQ < \sqrt{\frac{36}{5}}$.
(1)设直线AB的函数表达式为$y = kx + b(k \neq 0)$.所以$\begin{cases}-4k + b = 0\\b = 3\end{cases}$,解得$\begin{cases}k = \frac{3}{4}\\b = 3\end{cases}$.所以直线AB的函数表达式为$y = \frac{3}{4}x + 3$.
(2)因为$\angle BAO = \angle PAQ$,所以$\angle BAO - \angle PAO = \angle PAQ - \angle PAO$,即$\angle BAP = \angle OAQ$.因为$AP = AQ$,所以当$AC = AO = 3$时,$\triangle ACP \cong \triangle AOQ$.因为点$C(m,\frac{3}{4}m + 3)$,所以$m^{2} + (3 - \frac{3}{4}m - 3)^{2} = 3^{2}$,解得$m = -\frac{12}{5}$或$m = \frac{12}{5}$(舍去).所以当m的值为$-\frac{12}{5}$时,$\triangle ACP \cong \triangle AOQ$.
(3)①存在.如图1,若点C与点B重合,则点P在点$P'$处,与点B重合,点Q在y轴上的点$Q'$处.由
(2)得,$\angle P'AP = \angle Q'AQ$.又因为$AP = AQ$,$AP' = AQ'$,所以$\triangle P'AP \cong \triangle Q'AQ$,所以$\angle AQ'Q = \angle AP'P = \angle ABP$为定角.所以点Q在以$Q'$为端点的射线上运动(不包括点$Q'$),所以在y轴上存在一点D,使得$\angle ADQ$的大小始终不发生变化,此时点D与点$Q'$重合.因为$AD = AP' = AB = \sqrt{OA^{2} + OB^{2}} = 5$,所以点$D(0, -2)$.
②$\frac{6}{5} \leq OQ < \sqrt{\frac{36}{5}}$. 提示:如图2,由①知,点Q在射线DV上运动(不包括点D).过点O作$OE \perp DV$于点E,当点Q运动到点E时,OQ的值最小,设DV交x轴于点H.因为$\angle ADV = \angle ABO$,所以$\angle DOE = \angle BCP$,所以$\angle AOE = \angle ACP$.因为$\angle CAP = \angle OAE$,$AP = AE$,所以$\triangle CAP \cong \triangle OAE$.所以$OA = CA = 3$,$OE = CP$.同
(2),得点$C(-\frac{12}{5},\frac{6}{5})$,所以$OE = CP = \frac{6}{5}$.如图3,当点C运动到点A时,点Q运动到点F,此时$\angle BAO = \angle FAO$,$AF \perp DV$,$OQ$的值最大.作点F关于y轴的对称点G,此时点G落在线段AB上,可得$AF = OA = AG = 3$,$OF = OG$.由
(2),得点$G(-\frac{12}{5},\frac{6}{5})$,所以$OF = OG = \sqrt{(-\frac{12}{5})^{2} + (\frac{6}{5})^{2}} = \sqrt{\frac{36}{5}}$.因为点C不与点A重合,所以$OQ < \sqrt{\frac{36}{5}}$.
10. 在甲、乙两地之间有一服务区,一辆客车从甲地驶往乙地,一辆货车从乙地驶往甲地. 两车同时出发,匀速行驶,客车、货车离服务区的距离$y_1(km),y_2(km)$与行驶的时间x(h)之间的函数关系如图1所示.
(1)甲、乙两地相距
(2)求出发3h后,货车离服务区的距离$y_2(km)$与行驶时间x(h)之间的函数表达式.
(3)在客车和货车出发的同时,有一辆邮政车从服务区匀速去甲地取货后返回乙地(取货的时间忽略不计),邮政车离服务区的距离$y_3(km)$与行驶时间x(h)之间的函数关系如图2中的虚线所示,请直接写出在行驶的过程中,经过多长时间邮政车与客车和货车的距离相等.
(1)甲、乙两地相距
480
km.(2)求出发3h后,货车离服务区的距离$y_2(km)$与行驶时间x(h)之间的函数表达式.
解:设3 h后,货车离服务区的距离$y_2$与行驶时间x之间的函数表达式为$y_2 = kx + b(k \neq 0)$。由题图可得,货车的速度为$120 ÷ 3 = 40(km/h)$,则点B的横坐标为$3 + 360 ÷ 40 = 12$,所以点B的坐标为$(12,360)$。所以$\begin{cases}3k + b = 0\\12k + b = 360\end{cases}$,解得$\begin{cases}k = 40\\b = -120\end{cases}$。即3 h后,货车离服务区的距离$y_2$与行驶时间x之间的函数表达式为$y_2 = 40x - 120(3 < x \leq 12)$。
(3)在客车和货车出发的同时,有一辆邮政车从服务区匀速去甲地取货后返回乙地(取货的时间忽略不计),邮政车离服务区的距离$y_3(km)$与行驶时间x(h)之间的函数关系如图2中的虚线所示,请直接写出在行驶的过程中,经过多长时间邮政车与客车和货车的距离相等.
经过1.2 h或4.8 h或7.5 h,邮政车与客车和货车的距离相等。
答案:
解:
(1)480
(2)设3 h后,货车离服务区的距离$y_2$与行驶时间x之间的函数表达式为$y_2 = kx + b(k \neq 0)$.由题图可得,货车的速度为$120 ÷ 3 = 40(km/h)$,则点B的横坐标为$3 + 360 ÷ 40 = 12$,所以点B的坐标为$(12,360)$.所以$\begin{cases}3k + b = 0\\12k + b = 360\end{cases}$,解得$\begin{cases}k = 40\\b = -120\end{cases}$.即3 h后,货车离服务区的距离$y_2$与行驶时间x之间的函数表达式为$y_2 = 40x - 120(3 < x \leq 12)$.
(3)经过1.2 h或4.8 h或7.5 h,邮政车与客车和货车的距离相等. 提示:$v_{客} = 360 ÷ 6 = 60(km/h)$,$v_{邮} = 360 × 2 ÷ 8 = 90(km/h)$.客车$\frac{360 + 120}{60} = 8(h)$到达乙地,邮政车$\frac{360 × 2 + 120}{90} = \frac{28}{3}(h)$到达乙地,货车12 h到达甲地.
设当邮政车去甲地的途中时,经过$t(0 < t \leq 4)h$邮政车与客车和货车的距离相等,则$360 - (60 + 90)t = 120 + (90 - 40)t$,解得$t = 1.2$;当客车和货车相遇时,邮政车与客车和货车的距离相等,即$60t + 40t = 480$,解得$t = 4.8$;设当邮政车从甲地返回乙地时,经过$t(4 < t \leq 4.8)h$邮政车与客车和货车的距离相等,则邮政车必超越客车,故$90t - 360 - 60t > 0$,解得$t > 12$,矛盾;若经过$t(4.8 < t \leq 8)h$邮政车与客和货车的距离相等,则有$60t + 40t - 480 = 2[60t - (90t - 360)]$,$t = 7.5$;若$8 \leq t \leq \frac{28}{3}$,则客车到达乙地停驶,有$40t = 2[480 - (90t - 360)]$,$t = \frac{84}{11} < 8$,舍去;若$\frac{28}{3} < t \leq 12$,此时客车与邮政车到达乙地,货车已离开乙地但未到达甲地,不符合题意,舍去.
(1)480
(2)设3 h后,货车离服务区的距离$y_2$与行驶时间x之间的函数表达式为$y_2 = kx + b(k \neq 0)$.由题图可得,货车的速度为$120 ÷ 3 = 40(km/h)$,则点B的横坐标为$3 + 360 ÷ 40 = 12$,所以点B的坐标为$(12,360)$.所以$\begin{cases}3k + b = 0\\12k + b = 360\end{cases}$,解得$\begin{cases}k = 40\\b = -120\end{cases}$.即3 h后,货车离服务区的距离$y_2$与行驶时间x之间的函数表达式为$y_2 = 40x - 120(3 < x \leq 12)$.
(3)经过1.2 h或4.8 h或7.5 h,邮政车与客车和货车的距离相等. 提示:$v_{客} = 360 ÷ 6 = 60(km/h)$,$v_{邮} = 360 × 2 ÷ 8 = 90(km/h)$.客车$\frac{360 + 120}{60} = 8(h)$到达乙地,邮政车$\frac{360 × 2 + 120}{90} = \frac{28}{3}(h)$到达乙地,货车12 h到达甲地.
设当邮政车去甲地的途中时,经过$t(0 < t \leq 4)h$邮政车与客车和货车的距离相等,则$360 - (60 + 90)t = 120 + (90 - 40)t$,解得$t = 1.2$;当客车和货车相遇时,邮政车与客车和货车的距离相等,即$60t + 40t = 480$,解得$t = 4.8$;设当邮政车从甲地返回乙地时,经过$t(4 < t \leq 4.8)h$邮政车与客车和货车的距离相等,则邮政车必超越客车,故$90t - 360 - 60t > 0$,解得$t > 12$,矛盾;若经过$t(4.8 < t \leq 8)h$邮政车与客和货车的距离相等,则有$60t + 40t - 480 = 2[60t - (90t - 360)]$,$t = 7.5$;若$8 \leq t \leq \frac{28}{3}$,则客车到达乙地停驶,有$40t = 2[480 - (90t - 360)]$,$t = \frac{84}{11} < 8$,舍去;若$\frac{28}{3} < t \leq 12$,此时客车与邮政车到达乙地,货车已离开乙地但未到达甲地,不符合题意,舍去.
查看更多完整答案,请扫码查看


