《2025年小题狂做八年级数学上册苏科版巅峰版》

10. 如图,在四边形ABCD中,AB= AC,BC= BD.若∠ABC= 1/2∠BAD= α,则∠BCD= ______(用含α的代数式表示).

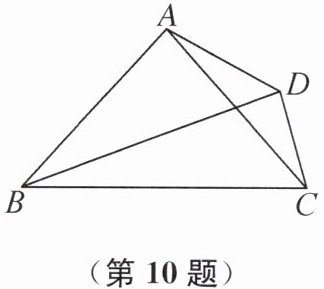
180° - 2α

答案： 180° - 2α　提示:延长DA至点M，使AM=AB,连接BM.因为AB=AC,所以AM=AB=AC,∠ACB=∠ABC=α,所以∠BAC=180° - 2α.因为∠BAD=2α,所以∠BAM=180° - ∠BAD=180° - 2α,所以∠BAC=∠BAM.所以∠CAD=180° - 2∠BAC=4α - 180°.在△MAB和△CAB 中,$\begin{cases} AM=AC, \\ ∠BAM=∠BAC, \\ AB=AB, \end{cases}$所以△MAB≌△CAB,所以∠M=∠ACB=α,BM=BC=BD,所以∠ADB=∠M=∠ACB=α.因为∠DBC+∠ACB=∠CAD+∠ADB,所以∠DBC=∠CAD=4α - 180°,所以∠BCD=$\frac{180° - ∠DBC}{2}$=90° - $\frac{1}{2}$∠DBC=90° - $\frac{1}{2}$(4α - 180°)=180° - 2α.

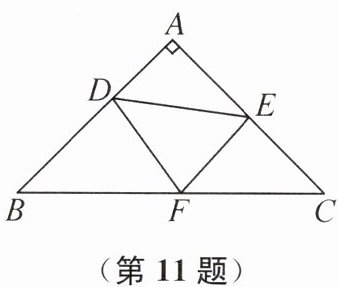
11. 如图,在△ABC中,AB= AC,∠BAC= 90°,D为AB上一定点,E,F分别为边AC,BC上的动点.当△DEF的周长最小时,∠FDE的度数为______90°.

答案： 90°　提示:分别作点D关于AC的对称点G,关于BC的对称点H,连接GH交AC,BC于点E₁，F₁,连接DE₁,DF₁.则DE₁=E₁G,DF₁=F₁H,此时△DEF的周长最小,最小值为GH的长,∠FDE的度数为∠F₁DE₁的度数.因为AB=AC,∠BAC=90°,所以∠C=∠B=45°.因为DH⊥BC,所以∠BDH=90° - ∠B=45°.由外角的性质,得∠BDH=∠DGE₁+∠DHF₁=45°,因为DE₁=E₁G,DF₁=F₁H,所以∠E₁DG=∠DGE₁,∠F₁DH=∠DHF₁,所以∠E₁DG+∠F₁DH=45°,所以∠F₁DE₁=180° - ∠BDH - ∠E₁DG - ∠F₁DH=90°.

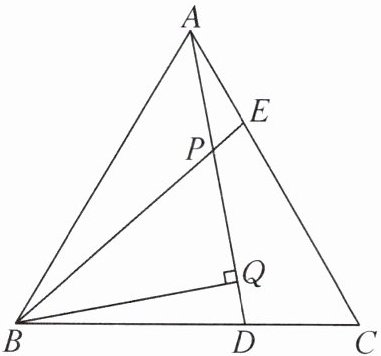
12. 如图,△ABC为等边三角形,AE= CD,AD,BE相交于点P,BQ⊥AD于点Q.
(1)求证：△ADC≌△BEA.
(2)求∠BPQ的度数.
(3)若PQ= 4,PE= 1,求AD的长.

答案：
(1)证明:因为△ABC为等边三角形,所以AB=CA,∠BAE=∠C=60°.在$\begin{cases} AB=CA, \\ ∠BAE=∠C, \\ AE=CD, \end{cases}$所以△ADC≌△BEA(SAS).
(2)解:由
(1)知,△ADC≌△BEA,所以∠ABE=∠CAD,所以∠BAD+∠ABP=∠BAD+∠CAD=∠BAC=60°,所以∠BPQ=∠BAD+∠ABP=60°.
(3)解:由
(1)知,△ADC≌△BEA,所以AD=BE.由
(2)知∠BPQ=60°.因为BQ⊥AD,所以∠PBQ=30°,所以BP=2PQ=8,所以BE=BP+PE=9,即AD=9.

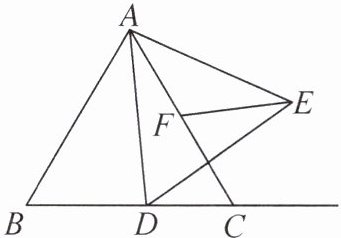
13. 如图,等边三角形ABC的边长为4,动点D从点B出发,沿射线BC方向移动,以AD为边在右侧作等边三角形ADE,取AC的中点F,连接EF.当EF的值最小时,BD= ______1.

答案： 1　提示:如图，连接CE.因为△ABC,△ADE均为等边三角形,所以AB=AC,AD=AE,∠BAC=∠DAE=∠ABC=∠ACB=60°.所以∠BAD=∠CAE,所以△BAD≌△CAE.所以BD=CE,∠ACE=∠ABC=∠BAC=60°,所以CE//AB.过点F作FH⊥CE,垂足为H.当点E与点H重合时,EF的值最小.因为∠ACH=60°,∠FHC=90°,所以∠CFH=30°.因为CF=$\frac{1}{2}$AC=2,所以CH=$\frac{1}{2}$CF=1.所以BD=CE=1(点E与点H重合).

14. 如图,在四边形ABCD中,∠BAD= α,∠C= 180°-α,BD平分∠ABC.
(1)如图1,若α= 90°,根据教材中的一个重要性质,直接可得AD= CD,这个性质是角平分线上的点到角两边的距离相等.
(2)问题解决：如图2,求证：AD= CD.
证明:过点D分别作DE⊥BA，交BA的延长线于点E,DF⊥BC于点F.因为BD平分∠ABC,DE⊥BE,DF⊥BF,所以DE=DF.因为∠BAD+∠C=180°,∠BAD+∠EAD=180°,所以∠EAD=∠C.在$\begin{cases} ∠DEA=∠DFC, \\ ∠EAD=∠C, \\ DE=DF, \end{cases}$所以△DEA≌△DFC,所以AD=CD.
(3)问题拓展：如图3,在等腰三角形ABC中,∠A= 100°,BD平分∠ABC,求证：BD+AD= BC.
证明:在BC上截取BK=BD,连接DK.因为AB=AC,∠A=100°,所以∠ABC=∠C=40°.因为BD平分∠ABC,所以∠DBK=$\frac{1}{2}$∠ABC=20°.因为BD=BK,所以∠BKD=∠BDK=80°,即∠A+∠BKD=180°.由(2)得AD=DK.因为∠BKD=∠C+∠KDC,所以∠KDC=∠C=40°,所以DK=CK,所以AD=DK=CK.所以BD+AD=BK+CK=BC.

答案：
(1)角平分线上的点到角两边的距离相等
(2)证明:过点D分别作DE⊥BA，交BA的延长线于点E,DF⊥BC于点F.因为BD平分∠ABC,DE⊥BE,DF⊥BF,所以DE=DF.因为∠BAD+∠C=180°,∠BAD+∠EAD=180°,所以∠EAD=∠C.在$\begin{cases} ∠DEA=∠DFC, \\ ∠EAD=∠C, \\ DE=DF, \end{cases}$所以△DEA≌△DFC,所以AD=CD.
(3)证明:在BC上截取BK=BD,连接DK.因为AB=AC,∠A=100°,所以∠ABC=∠C=40°.因为BD平分∠ABC,所以∠DBK=$\frac{1}{2}$∠ABC=20°.因为BD=BK,所以∠BKD=∠BDK=80°,即∠A+∠BKD=180°.由
(2)得AD=DK.因为∠BKD=∠C+∠KDC,所以∠KDC=∠C=40°,所以DK=CK,所以AD=DK=CK.所以BD+AD=BK+CK=BC.