第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
8. 如图1,直线$AB过点C(2,-4)$,且与$y轴交于点B(0,-8)$,与$x轴交于点A$.
(1)求直线$AB的函数表达式及点A$的坐标.
(2)如图2,作直线$OC$,点$P在直线OC$上,当$\triangle PBC的面积为\triangle BOC$面积的2倍时,求点$P$的坐标.
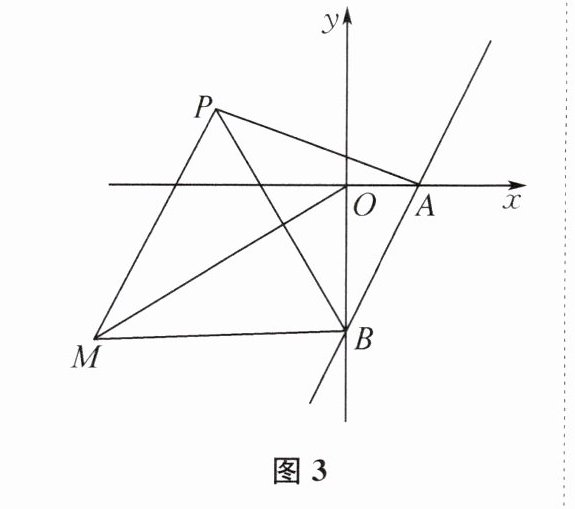
(3)如图3,$P$为第二象限内的一点,连接$BP$,以$BP为边在BP的左侧作等边\triangle PBM$,当$\angle MOB= 60^{\circ}$,$OM= 8+4\sqrt{3}$时,求线段$PA$的长.
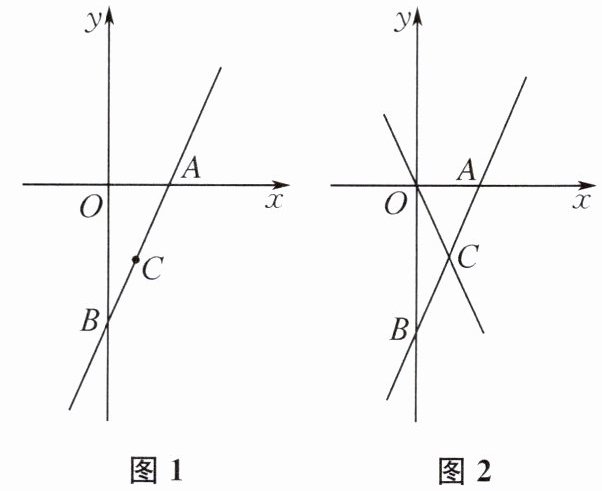
(1)求直线$AB的函数表达式及点A$的坐标.
(2)如图2,作直线$OC$,点$P在直线OC$上,当$\triangle PBC的面积为\triangle BOC$面积的2倍时,求点$P$的坐标.
(3)如图3,$P$为第二象限内的一点,连接$BP$,以$BP为边在BP的左侧作等边\triangle PBM$,当$\angle MOB= 60^{\circ}$,$OM= 8+4\sqrt{3}$时,求线段$PA$的长.


答案:
(1) 因为点$B(0,-8),C(2,-4)$,所以直线AB的函数表达式为$y=2x-8$,令$y=0$,则$x=4$,即点$A(4,0)$.
(2) 由点$C(2,-4)$,可得直线OC的函数表达式为$y=-2x$. 当点P在BC下方时,因为$S_{△PBC}=2S_{△BOC}$,所以$PO=3OC$. 设点$P(t,-2t)$,则$\sqrt {t^{2}+(-2t)^{2}}=3\sqrt {2^{2}+(-4)^{2}}$,解得$t=6$(负值已舍). 所以点$P(6,-12)$. 当点P在BC上方时,可知$PO=OC$,同理可得点$P(-2,4)$. 所以点P的坐标为$(6,-12)$或$(-2,4)$.
(3) 如图,在OM上截取$OG=OB=8$,连接OP,BG,过点P作$PH⊥x$轴于点H,则$GM=OM - OG=8+4\sqrt {3}-8=4\sqrt {3}$. 设BP交OM于点T. 因为$∠MOB=60^{\circ }$,所以$△OBG$为等边三角形. 因为$△PBM$为等边三角形,所以$BM=BP,∠MBG=60^{\circ }-∠GBT=∠PBO$. 因为$BG=BO$,所以$△BGM\cong △BOP(SAS)$,所以$∠BMG=∠BPO,OP=GM=4\sqrt {3}$. 因为$∠PTO=∠MTB,∠BMG=∠BPO$,所以$∠POM=∠PBM=60^{\circ }$,因为$∠HOM=90^{\circ }-∠MOB=30^{\circ }$,所以$∠POH=60^{\circ }-∠HOM=30^{\circ }$,所以$PH=\frac {1}{2}OP=2\sqrt {3}$,所以$OH=\sqrt {OP^{2}-PH^{2}}=6$,所以$PA=\sqrt {PH^{2}+AH^{2}}=\sqrt {(2\sqrt {3})^{2}+(6+4)^{2}}=4\sqrt {7}.$
(1) 因为点$B(0,-8),C(2,-4)$,所以直线AB的函数表达式为$y=2x-8$,令$y=0$,则$x=4$,即点$A(4,0)$.
(2) 由点$C(2,-4)$,可得直线OC的函数表达式为$y=-2x$. 当点P在BC下方时,因为$S_{△PBC}=2S_{△BOC}$,所以$PO=3OC$. 设点$P(t,-2t)$,则$\sqrt {t^{2}+(-2t)^{2}}=3\sqrt {2^{2}+(-4)^{2}}$,解得$t=6$(负值已舍). 所以点$P(6,-12)$. 当点P在BC上方时,可知$PO=OC$,同理可得点$P(-2,4)$. 所以点P的坐标为$(6,-12)$或$(-2,4)$.
(3) 如图,在OM上截取$OG=OB=8$,连接OP,BG,过点P作$PH⊥x$轴于点H,则$GM=OM - OG=8+4\sqrt {3}-8=4\sqrt {3}$. 设BP交OM于点T. 因为$∠MOB=60^{\circ }$,所以$△OBG$为等边三角形. 因为$△PBM$为等边三角形,所以$BM=BP,∠MBG=60^{\circ }-∠GBT=∠PBO$. 因为$BG=BO$,所以$△BGM\cong △BOP(SAS)$,所以$∠BMG=∠BPO,OP=GM=4\sqrt {3}$. 因为$∠PTO=∠MTB,∠BMG=∠BPO$,所以$∠POM=∠PBM=60^{\circ }$,因为$∠HOM=90^{\circ }-∠MOB=30^{\circ }$,所以$∠POH=60^{\circ }-∠HOM=30^{\circ }$,所以$PH=\frac {1}{2}OP=2\sqrt {3}$,所以$OH=\sqrt {OP^{2}-PH^{2}}=6$,所以$PA=\sqrt {PH^{2}+AH^{2}}=\sqrt {(2\sqrt {3})^{2}+(6+4)^{2}}=4\sqrt {7}.$
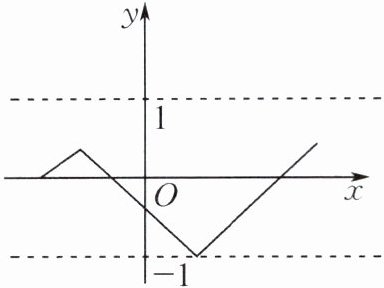
9. 对某一个函数给出如下定义:若存在实数$M>0$,对于这个函数的所有函数值$y$,都满足$-M\leqslant y\leqslant M$,则称这个函数是有界函数,在所有满足条件的$M$中,其最小值称为这个函数的边界值. 例如,图中的函数是有界函数,其边界值是1. 函数$y= x+1(-4\leqslant x\leqslant2)$的边界值为
若函数$y= -x+1(a\leqslant x\leqslant b,b>a)$的边界值是5,且这个函数的最大值也是5,则$b$的取值范围为
3
.若函数$y= -x+1(a\leqslant x\leqslant b,b>a)$的边界值是5,且这个函数的最大值也是5,则$b$的取值范围为
$-4 < b ≤ 6$
.
答案:
3 -4 < b ≤ 6 提示:函数$y=x+1(-4≤x≤2)$中,$-3≤y≤3$,所以其边界值为3. 因为$k=-1$,y随x的增大而减小,所以当$x=a$时,$-a+1=5$,解得$a=-4$,而$x=b$时,$y=-b+1$,所以$-5≤-b+1≤5$,且$b>a$,所以$-4 < b ≤ 6.$
10. 对于点$P$,直线$l和图形N$,给出如下定义:若点$P关于直线l的对称点P'在图形N$的内部或边上,则称$P为图形N关于直线l$的“镜像点”. 在平面直角坐标系$xOy$中,已知$\triangle ABC的三个顶点的坐标分别为A(2,1),B(-1,1),C(-1,-2)$,设点$T(0,t)$,$l_{1}为过点T(0,t)且与y$轴垂直的直线.
(1)若$t= -2$,在点$P_{1}(0,-4),P_{2}(2,-5.5),P_{3}(-1,-2.2)$中,
(2)当$t\neq0$时,若$x轴上存在\triangle ABC关于直线l_{1}$的“镜像点”,则$t$的最小值为
(3)已知直线$l_{2}过点T(0,t)$且与第一、三象限的角平分线平行.
①若直线$l_{2}上存在\triangle ABC关于直线l_{1}$的“镜像点”,直接写出$t$的取值范围;
②已知边长为1的正方形$DEFH的对角线的交点为Q(t,0)$,且正方形$DEFH$的边与坐标轴平行. 若正方形$DEFH边上的所有点都是\triangle ABC关于直线l_{2}$的“镜像点”,直接写出$t$的取值范围.
(1)若$t= -2$,在点$P_{1}(0,-4),P_{2}(2,-5.5),P_{3}(-1,-2.2)$中,
$P_{1},P_{3}$
(填字母)是$\triangle ABC关于直线l_{1}$的“镜像点”.(2)当$t\neq0$时,若$x轴上存在\triangle ABC关于直线l_{1}$的“镜像点”,则$t$的最小值为
-1
.(3)已知直线$l_{2}过点T(0,t)$且与第一、三象限的角平分线平行.
①若直线$l_{2}上存在\triangle ABC关于直线l_{1}$的“镜像点”,直接写出$t$的取值范围;
$-3≤t≤3$
②已知边长为1的正方形$DEFH的对角线的交点为Q(t,0)$,且正方形$DEFH$的边与坐标轴平行. 若正方形$DEFH边上的所有点都是\triangle ABC关于直线l_{2}$的“镜像点”,直接写出$t$的取值范围.
$0≤t≤\frac {1}{4}$
答案:
(1)$P_{1},P_{3}$
(2) -1 提示:设x轴上点$(a,0)$,关于直线$y=t$的对称点为$(a,2t)$,所以$-2≤2t≤1$,所以$-1≤t≤\frac {1}{2}$,所以t的最小值为-1.
(3)①$-3≤t≤3$. 提示:由题意设直线$l_{2}$的函数表达式为$y=x+t$,则$l_{2}$关于直线$y=t$的“镜像”的直线$l'_{2}$的函数表达式为$y=-x+t$. 如图1,当直线$l'_{2}$过点$A(2,1)$时,$1=-2+t$,所以$t=3$,当直线$l'_{2}$过点$C(-1,-2)$时,$-2=-(-1)+t$,所以$t=-3$,所以$-3≤t≤3.$②$0≤t≤\frac {1}{4}$. 提示:由点$A(2,1),C(-1,-2)$,可得直线AC的函数表达式为$y=x-1$. 因为点Q关于$l_{2}$的对称点$I(-t,2t)$,所以正方形DEFH关于$l_{2}$的对称正方形MNGH的各点坐标为$M(-t-\frac {1}{2},2t+\frac {1}{2}),N(-t+\frac {1}{2},2t+\frac {1}{2}),G(-t+\frac {1}{2},2t-\frac {1}{2}),H(-t-\frac {1}{2},2t-\frac {1}{2})$. 如图2,因为正方形DEFH边上的所有点都是$△ABC$关于直线$l_{2}$的“镜像点”,所以$\begin{cases}2t+\frac {1}{2}≤1\\-t-\frac {1}{2}≥-1\\-t+\frac {1}{2}-1≤2t-\frac {1}{2}\end{cases}$,所以$0≤t≤\frac {1}{4}.$
(1)$P_{1},P_{3}$
(2) -1 提示:设x轴上点$(a,0)$,关于直线$y=t$的对称点为$(a,2t)$,所以$-2≤2t≤1$,所以$-1≤t≤\frac {1}{2}$,所以t的最小值为-1.
(3)①$-3≤t≤3$. 提示:由题意设直线$l_{2}$的函数表达式为$y=x+t$,则$l_{2}$关于直线$y=t$的“镜像”的直线$l'_{2}$的函数表达式为$y=-x+t$. 如图1,当直线$l'_{2}$过点$A(2,1)$时,$1=-2+t$,所以$t=3$,当直线$l'_{2}$过点$C(-1,-2)$时,$-2=-(-1)+t$,所以$t=-3$,所以$-3≤t≤3.$②$0≤t≤\frac {1}{4}$. 提示:由点$A(2,1),C(-1,-2)$,可得直线AC的函数表达式为$y=x-1$. 因为点Q关于$l_{2}$的对称点$I(-t,2t)$,所以正方形DEFH关于$l_{2}$的对称正方形MNGH的各点坐标为$M(-t-\frac {1}{2},2t+\frac {1}{2}),N(-t+\frac {1}{2},2t+\frac {1}{2}),G(-t+\frac {1}{2},2t-\frac {1}{2}),H(-t-\frac {1}{2},2t-\frac {1}{2})$. 如图2,因为正方形DEFH边上的所有点都是$△ABC$关于直线$l_{2}$的“镜像点”,所以$\begin{cases}2t+\frac {1}{2}≤1\\-t-\frac {1}{2}≥-1\\-t+\frac {1}{2}-1≤2t-\frac {1}{2}\end{cases}$,所以$0≤t≤\frac {1}{4}.$
查看更多完整答案,请扫码查看


