《2025年小题狂做八年级数学上册苏科版巅峰版》

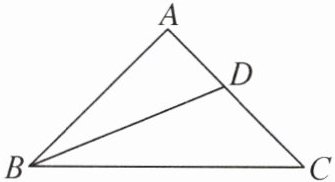
9. 如图,BD 是△ABC 的角平分线,AB = AC.若 BC= AB+AD,则∠A= ______.

90°

答案： 90° 提示:在BC上截取BE=AB,连接DE.因为BC=AB+AD,所以CE=AD.因为BD是△ABC的角平分线，所以∠ABD=∠EBD.因为AB=EB,BD=BD,所以△ABD≌△EBD,所以AD=ED=CE,∠A=∠DEB,所以∠C=∠EDC,所以∠A=∠DEB=∠C+∠EDC=2∠C.因为AB=AC,所以∠C=∠ABC.因为∠A+∠ABC+∠C=180°,所以4∠C=180°,所以∠C=45°,∠A=2∠C=90°.

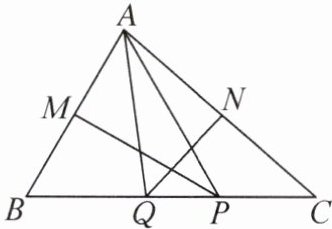
10. 在△ABC 中,AB 的垂直平分线分别交线段 AB,BC 于点 M,P,AC 的垂直平分线分别交线段 AC,BC 于点 N,Q.
(1) 如图,当∠BAC= 80°时,求∠PAQ 的度数.
(2) 当∠BAC 满足什么条件时,AP ⊥ AQ？请说明理由.
(3) 在(2)的条件下,若 BC = 10,求△APQ 的周长.

答案：
解:
(1)因为MP，NQ分别是AB，AC的垂直平分线,所以AP=BP,AQ=CQ,所以∠BAP=∠B,∠CAQ=∠C.因为∠BAC=80°,所以∠B+∠C=180°−∠BAC=100°.所以∠PAQ=∠BAP+∠CAQ−∠BAC=∠B+∠C−∠BAC=20°.
(2)当∠BAC=135°时,AP⊥AQ.理由如下:
如图,因为AP⊥AQ,所以∠PAQ=90°.由
(1)得∠BAP=∠B,∠CAQ=∠C.又因为∠B+∠C=180°−∠BAC,∠BAP+∠CAQ=∠BAC−90°,所以180°−∠BAC=∠BAC−90°,所以∠BAC=135°.

(3)因为△APQ的周长为AP+PQ+AQ=BP+PQ+CQ=BC,BC=10,所以△APQ的周长为10.

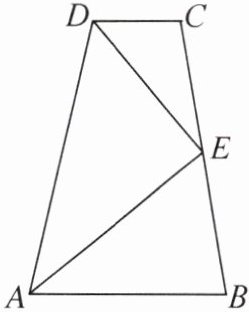
11. 如图,在四边形 ABCD 中,AB//CD,E 是 BC 的中点,DE 平分∠ADC.求证:AE 是∠DAB 的平分线.

答案：
证明:如图,过点E分别作EF⊥AD于点F,EH⊥AB于点H,反向延长EH,交DC的延长线于点G.因为AB//CD,EH⊥AB,所以EG⊥DC,∠CGE=∠BHE=90°.因为E是BC的中点,所以CE=BE.在△CGE与△BHE中,$\begin{cases} \angle CGE=\angle BHE \\ CE=EB \\ \angle CEG=\angle BEH \end{cases}$所以△CGE≌△BHE,所以EG=EH.因为DE平分∠ADC,所以EG=EF,所以EF=EH,所以AE是∠DAB的平分线.

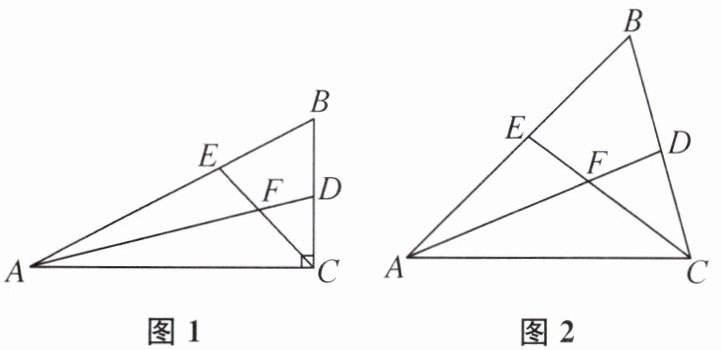
12. 如图 1,在△ABC 中,∠ACB= 90°,∠B= 60°,AD,CE 分别是∠BAC,∠BCA 的平分线,AD,CE 相交于点 F.
(1) 求证:∠BEC= ∠ADC.
(2) 请你判断 FE 与 FD 之间的数量关系,并证明.
(3) 如图 2,在△ABC 中,如果∠ACB 不是直角,∠B= 60°,AD,CE 分别是∠BAC,∠BCA 的平分线,AD,CE 相交于点 F.FE= FD 是否仍然成立？若成立,请证明;若不成立,请说明理由.

答案：

(1)证明:因为AD,CE分别是∠BAC,∠BCA的平分线,所以∠DAC=∠DAB=$\frac{1}{2}\angle BAC=\frac{1}{2}(90^{\circ}-\angle B)=15^{\circ}$,$\angle ACE=\frac{1}{2}\angle ACB=45^{\circ}$,所以∠ADC=∠BAD+∠B=75°,∠BEC=∠BAC+∠ACE=75°,所以∠BEC=∠ADC.
(2)解:FE=FD.证明如下:
如图1,过点F分别作FH⊥BC于点H，FG⊥AB于点G,连接BF.因为F是△ABC两条角平分线的交点，所以BF也是△ABC的角平分线，所以HF=GF，∠DHF=∠EGF=90°.由
(1)知,∠HDF=∠GEF.在△EGF和△DHF中,$\begin{cases} \angle EGF=\angle DHF \\ \angle GEF=\angle HDF \\ GF=HF \end{cases}$所以△EGF≌△DHF(AAS),所以FE=FD.

(3)解:成立.证明如下:
如图2,过点F分别作FM⊥BC于点M,FN⊥AB于点N,连接BF.同理
(2)可得MF=NF,∠DMF=∠ENF=90°.因为∠ABC=60°,所以∠MFN=180°−∠ABC=120°.因为∠CFA=180°−(∠FAC+∠FCA)=180°−$\frac{1}{2}$(∠CAB+∠ACB)=180°−$\frac{1}{2}$(180°−∠ABC)=120°,所以∠DFE=∠CFA=∠MFN.又因为∠MFN=∠MFD+∠DFN,∠DFE=∠DFN+∠NFE,所以∠MFD=∠NFE.在△ENF和△DMF中,$\begin{cases} \angle ENF=\angle DMF \\ NF=MF \\ \angle NFE=\angle MFD \end{cases}$所以△ENF≌△DMF(ASA),所以FE=FD.