《2025年小题狂做八年级数学上册苏科版巅峰版》

1. 如图,秋千静止时,踏板离地的垂直高度BE= 1m,将它往前推6m至点C处时(即水平距离CD= 6m),踏板离地的垂直高度CF= 4m,它的绳索始终拉直,则绳索AC的长是(B)
A.$\frac{21}{2}$m
B.$\frac{15}{2}$m
C.6m
D.$\frac{9}{2}$m

答案： B

2. 如图,在Rt△ABC中,∠ACB= 90°,AC= 3,BC= 4,BE平分∠ABC,CD⊥AB于点D,BE与CD相交于点F,则CF的长是(B)
A.1
B.$\frac{4}{3}$
C.$\frac{5}{3}$
D.2

答案： B　提示:过点E作EG⊥AB于点G.因为CD⊥AB于点D,所以EG//CD,所以∠GEB=∠EFC.因为∠ACB=90°,所以EC⊥BC.又因为BE平分∠ABC,EG⊥AB,所以EG=EC.在Rt△ABC中,AB=√(AC²+BC²)=5.易证Rt△EBC≌Rt△EBG,所以∠CEB=∠GEB,BG=BC=4.所以∠CEB=∠EFC,AG=AB−BG=1,所以CF=EC.设CF=EG=EC=x,则AE=3−x.在Rt△AEG中,由勾股定理,得(3−x)²=x²+1²,解得x=4/3.所以CF的长是4/3.

3. 已知:如图,在△ABC中,AB= 13,AC= 5,△ABC的周长为30.过点C作CD⊥AB于点D,E为边AB上的一点,且CE= BE,过点E作EF⊥AB交∠ACB的角平分线于点F.则线段EF的长为(A)
A.$\frac{13}{2}$
B.$\frac{15}{2}$
C.6
D.$\frac{9}{2}$

答案： A　提示:因为BC=30−AB−AC=12,所以AC²+BC²=AB²,所以∠ACB=90°.因为CD⊥AB,所以∠ACD=90°−∠BCD=∠B.因为CE=BE,所以∠BCE=∠B,所以∠ACD=∠BCE.因为CF是∠ACB的平分线,所以∠DCF=∠ECF.因为CD⊥AB,EF⊥AB,所以CD//EF,所以∠DCF=∠F.所以∠F=∠ECF,所以EF=CE.因为∠A+∠B=90°,∠ACE+∠B=∠ACE+∠BCE=90°,所以∠A=∠ACE,AE=CE=BE.所以EF=CE=1/2 AB=13/2.

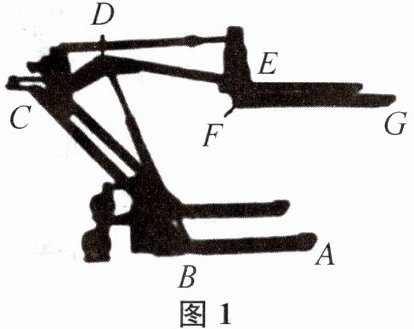
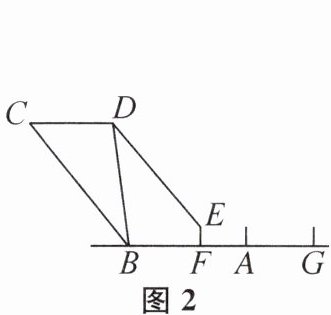
4. 图1是一辆卸货车实物图,折线A-B-C是支架,BD为可伸缩的液压支撑杆,测得BC= $\sqrt{10}$,CD= $\sqrt{2}$,DE= 3,∠ABC= ∠CDE= 135°,∠EFG= 90°.图2是卸货车不工作时的侧面示意图,此时AB与FG在同一直线上,CD//AB,且∠DEF= 135°,则BF= ______.

答案：
(5√2−2√5)/2　　提示:如图，过点D作DP⊥AB于点P,过点E作EM⊥DP于点M,过点C作CN⊥AB于点N.因为∠EFG=90°,∠DEF=135°,所以∠DEM=45°.在Rt△DEM中,EM=DM=3√2/2,即FP=EM=3√2/2,因为CN⊥PN,DP⊥NP,且CD=√2,所以FN=NP+FP=5√2/2.因为∠ABC=∠CDE=135°,所以∠CBN=45°,又因为BC=√10,所以NB=NC=√5.因为FB=FN−NB,所以BF=5√2/2−√5=(5√2−2√5)/2.

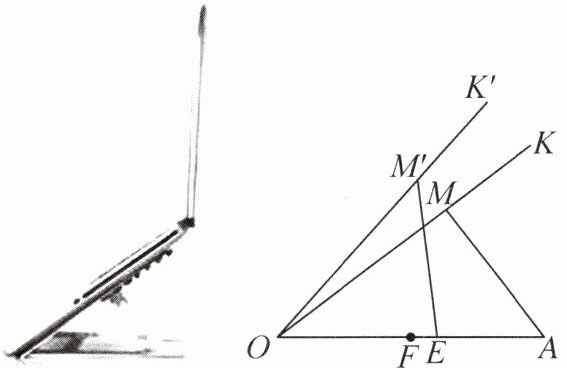
5. 如图是一种笔记本电脑支架,它有A～F共6个档位调节角度,相邻两个档位距离为2cm,已知托架OK的长度为24cm,M是支点且OM= 2MK.当支架调至点A时,AM⊥OK,当支架调至E档时,托架OK绕着点O旋转到OK',此时M'E= OE,则支点M'到OA的距离为______cm.

16√5/3

答案： 16√5/3　提示:由题意可知,MA=M'E=OE,AM⊥OK,AE=8cm.因为有A~F共6个档位调节角度,相邻两个档位距离为2cm,所以AE=8cm.因为OK=24cm,OM=2MK,所以OM=OM'=16cm.设MA=M'E=OE=xcm,则OA=(x+8)cm.在Rt△OAM中,由勾股定理,得OA²=MA²+OM²,即(x+8)²=x²+16²,解得x=12,所以MA=M'E=OE=12cm.过点M'作M'H⊥OA.设OH=ycm,则EH=(12−y)cm.由勾股定理,得M'H²=OM'²−OH²=M'E²−EH²,即16²−y²=12²−(12−y)²,解得y=32/3,所以M'H=√(OM'²−OH²)=16√5/3cm.

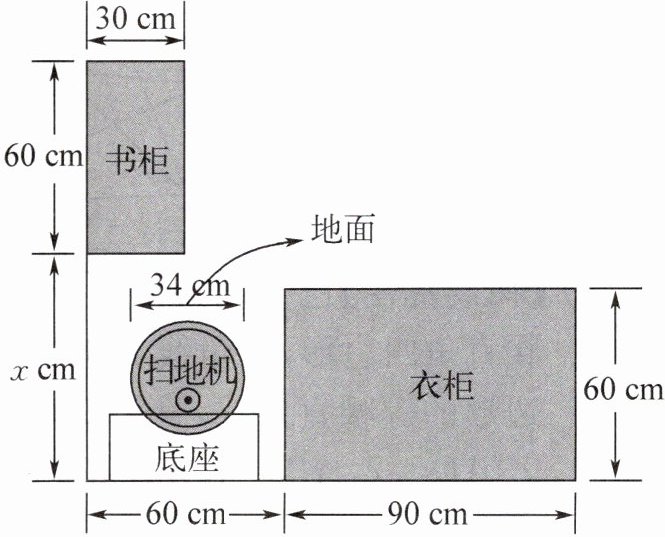
6. 如图,小红家购置了一台圆形自动扫地机,放置在屋子角落(书柜、衣柜与地面均无缝隙).在没有障碍物阻挡的前提下,扫地机能自动从底座脱离后打扫全屋地面.若这台扫地机能从角落自由进出,则图中的x至少为______.

76

答案： 76　　提示:由题意，得(x−60)²+(60 - 30)²≥34²,解得x≤44或x≥76.因为x＞60,所以图中的x至少为76.