《2025年小题狂做八年级数学上册苏科版巅峰版》

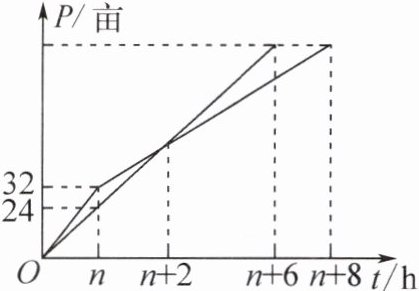
6. A,B两户同时对所承包的土地开始收割作业.在n h后,A户收割了32亩土地,B户收割了24亩土地.后因A户调走部分机器,导致收割速度变慢,B户按原先的速度匀速收割.他们收割的土地面积P(亩)与收割时间t(h)之间的函数关系如图所示,则B户收割亩数追上A户时,B户总共收割了______亩土地.

48

答案： 48　提示:设B户收割的土地面积P₁(亩)与收割时间t(h)之间的函数表达式为P₁ = kt(0≤t≤n + 6)，A户收割的土地面积P₂(亩)与收割时间t(h)之间的函数表达式为P₂ = $\begin{cases}mt(0≤t≤n)\\at + b(n＜t≤n + 8)\end{cases}$.因为P₁ = kt经过点(n,24)，所以k = $\frac{24}{n}$，即P₁ = $\frac{24}{n}$t.当t = n + 6时，P₁ = $\frac{24(n + 6)}{n}$.所以P₂ = at + b经过点(n,32)与点(n + 8,$\frac{24(n + 6)}{n}$).所以$\begin{cases}an + b = 32\\a(n + 8) + b = \frac{24(n + 6)}{n}\end{cases}$，解得$\begin{cases}a = \frac{18 - n}{n}\\b = 14 + n\end{cases}$.所以P₂ = $\frac{18 - n}{n}$t + 14 + n.又当t = n + 2时，两户收割的土地相同，所以$\frac{24(n + 2)}{n}$ = $\frac{18 - n}{n}$(n + 2) + 14 + n，解得n = 2.所以P₁ = $\frac{24}{2}$×(2 + 2) = 48.

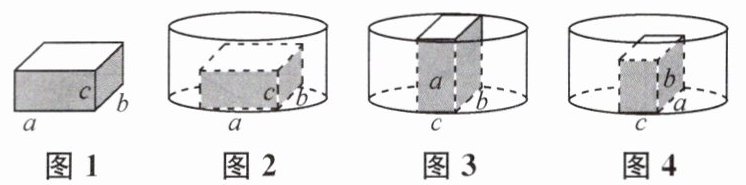
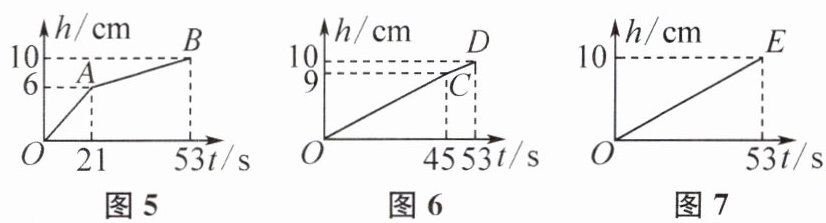
7. 将如图1所示的长方体石块$(a＞b＞c)$放入一圆柱形水槽内,并向水槽内匀速注水,速度为$vcm^{3}/s$,直至注满水槽为止.石块可以用三种不同的方式完全放入水槽内,如图2至图4所示,在这三种情况下,水槽内的水深h(cm)与注水时间t(s)之间的函数关系如图5至图7所示,根据图象解决下列问题:
(1)请分别将三种放置方式的示意图和与之相对应的函数关系图象用线连接起来.
(2)求图6中CD所在直线的函数表达式.
(3)求圆柱形水槽的底面积S.

答案： 解:
(1)题图2与题图5相对应，题图3与题图7相对应，题图4与题图6相对应，连线略.
(2)由题意可知，点C的坐标为(45,9)，点D的坐标为(53,10).设直线CD的函数表达式为h = kt + b(k≠0)，则$\begin{cases}9 = 45k + b\\10 = 53k + b\end{cases}$，解得$\begin{cases}k = \frac{1}{8}\\b = \frac{27}{8}\end{cases}$.所以直线CD的函数表达式为h = $\frac{1}{8}$t + $\frac{27}{8}$.
(3)由题图5、题图6和题图7可知水槽的高为10cm；由题图3和题图7可知石块的长a = 10cm；由题图4和题图6可知石块的宽b = 9cm；由题图2和题图5可知石块的高c = 6cm.所以石块的体积为abc = 540cm³.根据题图5和题图7可得$\begin{cases}21v = 6S - 540\\53v = 10S - 540\end{cases}$，解得$\begin{cases}v = 20\\S = 160\end{cases}$.所以圆柱形水槽的底面积S为160cm².