《2025年小题狂做八年级数学上册苏科版巅峰版》

1. 已知点$(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})在一次函数y= x+3$的图象上,且$x_{1}＜x_{2}＜x_{3}$,下列说法正确的是(A)
A.若$x_{1}x_{2}＜0$,则$y_{2}y_{3}＞0$
B.若$x_{1}x_{3}＜0$,则$y_{1}y_{2}＜0$
C.若$x_{2}x_{3}＜0$,则$y_{1}y_{2}＜0$
D.若$x_{2}x_{3}＜0$,则$y_{1}y_{2}＞0$

答案： A

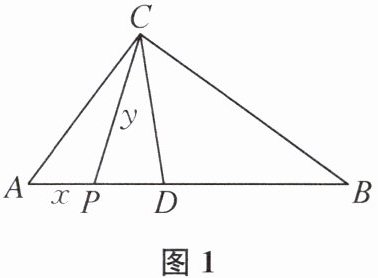
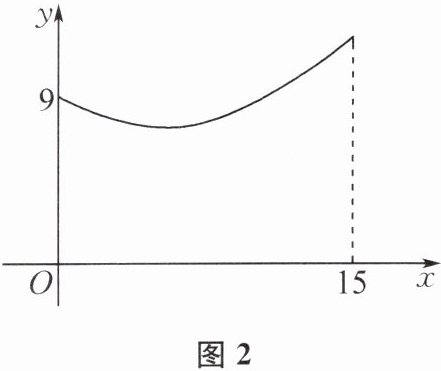
2. 如图1,在$\text{Rt}\triangle ABC$中,$\angle ACB= 90^{\circ}$,$CD$为角平分线.$P是边AB$上的一个动点,若$AP= x$,$CP= y$,则$y关于x$的函数图象如图2所示.现有下列结论:①斜边$AB$的长度为15;②斜边上高的长度为$\frac{36}{5}$;③斜边上中线的长度为$\frac{17}{2}$;$CD的长度为\frac{36\sqrt{2}}{7}$.其中所有正确结论的序号是______.


①②④

答案： ①②④ 提示:由题图2可知,当x=15时，y取得最大值,结合题图1可知,y的最大值在点P运动到点B处取得,此时AP=15=AB,故①正确.由题图2可知,当x=0时,y=9,即AC=9,所以BC=√(AB²-AC²)=√(15²-9²)=12.由等积法可知,斜边上的高的长度为(9×12)/15=36/5,故②正确.由直角三角形斜边上的中线等于斜边的一半,可知斜边AB上的中线长为15/2,故③错误.过点D分别作DE⊥AC于点E,DF⊥BC于点F,则DE=DF=(√2/2)CD.由等积法,可得AC·DE+BC·DF=AC·BC,所以CD=√2 DE=√2·(AC·BC)/(AC+BC)=36√2/7,故④正确.

3. 在平面直角坐标系中,$O$为坐标原点,$P(x,y)(xy\neq0)$是平面内任意一点.过点$P分别作x$轴、$y$轴的垂线,垂足分别为$M,N$.若四边形$PMON$的周长为6,则$P$叫作"周六点".例如,图中的$P(2,-1)$是一个"周六点".
(1) 若$D(m,2m+2)$为"周六点",求$m$的值.$m=-\dfrac{5}{3}$或$m=\dfrac{1}{3}$
(2) 已知点$Q的坐标为(2,2)$,若$P$是"周六点",则$PQ$长的最小值为A.
A. $\frac{\sqrt{2}}{2}$
B. 1
C. $\sqrt{2}$
D. 2
(3) 若一次函数$y= kx+k-4$的图象上存在"周六点",则$k$的取值范围是$k\geq1$或$k\lt-2$.

答案： 3. 解:
(1)由题意,得|m|+|2m+2|=3.①当m≤-1时,-m+(-2m-2)=3,解得m=-5/3.②当-1＜m≤0时,-m+2m+2=3.解得m=1(舍去).③当m＞0时,m+2m+2=3,解得m=1/3.综上所述,m=-5/3或m=1/3.
(2)A 提示:设点P(x,y),则|x|+|y|=3.易知其图象为如图所示的正方形EFGH(不含顶点),其中点E(0,3),F(3,0),即点P在正方形EFGH的边上运动.过点Q作QP'⊥EF于点P',则当点P与点P'重合时,PQ的值最小,最小值为P'Q的长.过点Q作QT//OE,交EF于点R,交OF于点T,则点R(2,1),T(2,0),所以RT=1,TF=1.所以△RTF为等腰直角三角形,所以∠QRP'=∠TRF=45°.在Rt△QP'R中,易得P'Q=P'R=(√2/2)QR=√2/2.
(3)k≥1或k＜-2 提示:如
(2)中图,一次函数y=kx+k-4=k(x+1)-4恒过定点L(-1,-4).易得直线LF的函数表达式为y=x-3(点G在直线LF上).易知点H(-3,0),可得直线LH的函数表达式为y=-2x-6.当所求的一次函数的k变化时,该函数图象绕着定点L旋转.观察图象,可知当k≥1或k＜-2时,该函数图象与正方形EFGH(不含顶点)有交点.