第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
10. 【阅读理解】课外小组活动时,老师提出了如下问题:在△ABC中,已知AB= 9,AC= 5,求边BC上的中线AD的取值范围.
(1)小明在组内经过合作交流,得到了如下的解决方法(图1):①延长AD至点Q,使得DQ= AD;②连接BQ,把AB,AC,2AD集中在△ABQ中;③利用三角形的三边关系,可得4<AQ<14,则AD的取值范围是
【感悟思考】解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)求图1中AC与BQ之间的位置关系,并加以证明.
(3)如图2,已知AD是△ABC的中线,AB= AE,AC= AF,∠BAE= ∠FAC= 90°,试探究线段AD与EF之间的位置关系和数量关系,并加以证明.
(1)小明在组内经过合作交流,得到了如下的解决方法(图1):①延长AD至点Q,使得DQ= AD;②连接BQ,把AB,AC,2AD集中在△ABQ中;③利用三角形的三边关系,可得4<AQ<14,则AD的取值范围是
2 < AD < 7
.【感悟思考】解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)求图1中AC与BQ之间的位置关系,并加以证明.
解:AC// BQ.证明如下:因为 AD 是△ABC的中线,所以BD = CD.在△QDB和△ADC中,$\left\{\begin{array}{l} BD = CD\\ ∠BDQ = ∠CDA\\ DQ = DA\end{array}\right.$,所以△QDB≌△ADC,所以∠BQD = ∠CAD,所以AC// BQ.
(3)如图2,已知AD是△ABC的中线,AB= AE,AC= AF,∠BAE= ∠FAC= 90°,试探究线段AD与EF之间的位置关系和数量关系,并加以证明.
解:AD⊥EF,AD = $\frac{1}{2}$EF.证明如下:延长 AD 至点 Q,使得DQ = AD,连接 BQ.由(2)得△QDB≌△ADC,所以BQ = CA.因为AC = AF,所以BQ = AF.由(2)得AC// BQ,所以∠BAC + ∠ABQ = 180°.因为∠BAE = ∠FAC = 90°,所以∠BAC + ∠EAF = 180°,所以∠ABQ = ∠EAF.易证△ABQ≌△EAF,所以AQ = EF,∠BAQ = ∠AEF.延长 DA 交 EF 于点 P. 因为∠BAE = 90°,所以∠BAQ + ∠EAP = 90°,所以∠AEF + ∠EAP = 90°,所以∠APE = 90°,所以AD⊥EF.因为AD = DQ,所以AQ = 2AD.因为AQ = EF,所以AD = $\frac{1}{2}$EF.
答案:
解:
(1)$2 < AD < 7$
(2)$AC// BQ$.证明如下:
因为 AD 是$\triangle ABC$的中线,所以$BD = CD$.
在$\triangle QDB$和$\triangle ADC$中,$\left\{\begin{array}{l} BD = CD\\ ∠BDQ = ∠CDA\\ DQ = DA\end{array}\right.$,所以$\triangle QDB\cong \triangle ADC$,所以$∠BQD = ∠CAD$,所以$AC// BQ$.
(3)$AD⊥EF,AD = \frac{1}{2}EF$.证明如下:
延长 AD 至点 Q,使得$DQ = AD$,连接 BQ.由
(2)得$\triangle QDB\cong \triangle ADC$,所以$BQ = CA$.因为$AC = AF$,所以$BQ = AF$.由
(2)得$AC// BQ$,所以$∠BAC + ∠ABQ = 180^{\circ }$.因为$∠BAE = ∠FAC = 90^{\circ }$,所以$∠BAC + ∠EAF = 180^{\circ }$,所以$∠ABQ = ∠EAF$.易证$\triangle ABQ\cong \triangle EAF$,所以$AQ = EF,∠BAQ = ∠AEF$.延长 DA 交 EF 于点 P. 因为$∠BAE = 90^{\circ }$,所以$∠BAQ + ∠EAP = 90^{\circ }$,所以$∠AEF + ∠EAP = 90^{\circ }$,所以$∠APE = 90^{\circ }$,所以$AD⊥EF$.因为$AD = DQ$,所以$AQ = 2AD$.因为$AQ = EF$,所以$AD = \frac{1}{2}EF$.
(1)$2 < AD < 7$
(2)$AC// BQ$.证明如下:
因为 AD 是$\triangle ABC$的中线,所以$BD = CD$.
在$\triangle QDB$和$\triangle ADC$中,$\left\{\begin{array}{l} BD = CD\\ ∠BDQ = ∠CDA\\ DQ = DA\end{array}\right.$,所以$\triangle QDB\cong \triangle ADC$,所以$∠BQD = ∠CAD$,所以$AC// BQ$.
(3)$AD⊥EF,AD = \frac{1}{2}EF$.证明如下:
延长 AD 至点 Q,使得$DQ = AD$,连接 BQ.由
(2)得$\triangle QDB\cong \triangle ADC$,所以$BQ = CA$.因为$AC = AF$,所以$BQ = AF$.由
(2)得$AC// BQ$,所以$∠BAC + ∠ABQ = 180^{\circ }$.因为$∠BAE = ∠FAC = 90^{\circ }$,所以$∠BAC + ∠EAF = 180^{\circ }$,所以$∠ABQ = ∠EAF$.易证$\triangle ABQ\cong \triangle EAF$,所以$AQ = EF,∠BAQ = ∠AEF$.延长 DA 交 EF 于点 P. 因为$∠BAE = 90^{\circ }$,所以$∠BAQ + ∠EAP = 90^{\circ }$,所以$∠AEF + ∠EAP = 90^{\circ }$,所以$∠APE = 90^{\circ }$,所以$AD⊥EF$.因为$AD = DQ$,所以$AQ = 2AD$.因为$AQ = EF$,所以$AD = \frac{1}{2}EF$.
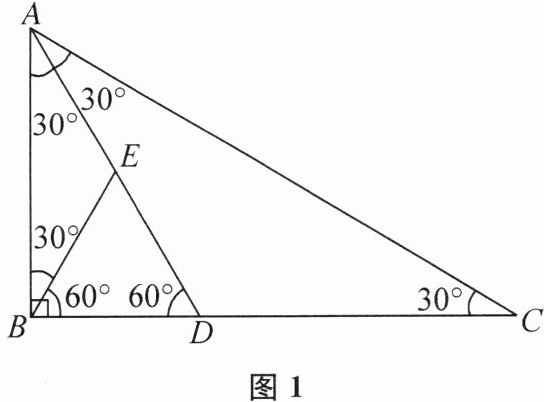
11. 定义:若一条线段将一个三角形分割成2个等腰三角形,则我们把这条线段叫作这个三角形的“双等腰线”;若两条线段将一个三角形分成3个等腰三角形,则我们把这两条线段叫作这个三角形的“三等腰线”. 如图1,BE是△ABD的“双等腰线”,AD,BE是△ABC的“三等腰线”.
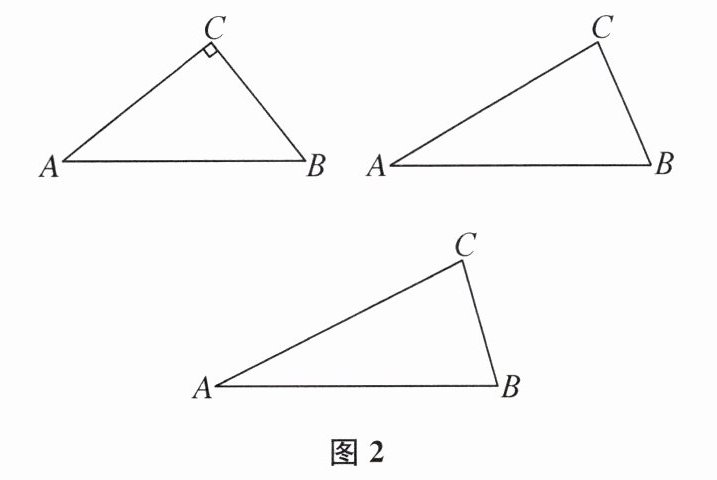
(1)请在下面三幅图中,分别画出△ABC的“双等腰线”,并做必要的标注或说明.
①∠C= 90°;②∠B= 70°,∠A= 35°;③∠B= 81°,∠A= 27°.
(2)如果一个等腰三角形有“双等腰线”,那么它的底角度数是______.
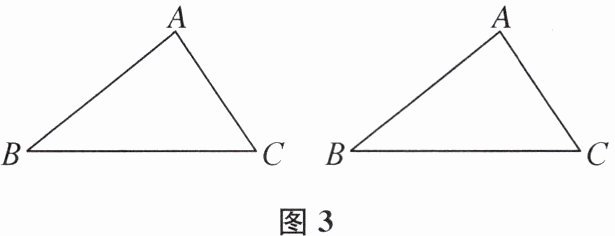
(3)如图3,在△ABC中,∠C= 3/2∠B,∠B<45°. 画出△ABC所有可能的“三等腰线”,使得对∠B取值范围内的任意值都成立,并做必要的标注或说明.(每种可能用一个图单独表示,如果图不够用可以自己补充)

(1)请在下面三幅图中,分别画出△ABC的“双等腰线”,并做必要的标注或说明.
①∠C= 90°;②∠B= 70°,∠A= 35°;③∠B= 81°,∠A= 27°.

(2)如果一个等腰三角形有“双等腰线”,那么它的底角度数是______.
(3)如图3,在△ABC中,∠C= 3/2∠B,∠B<45°. 画出△ABC所有可能的“三等腰线”,使得对∠B取值范围内的任意值都成立,并做必要的标注或说明.(每种可能用一个图单独表示,如果图不够用可以自己补充)

答案:
解:
(1) ①取线段 AB 的中点 D,连接 CD,则 CD 为$\triangle ABC$的“双等腰线”(图略).
②如图所示.
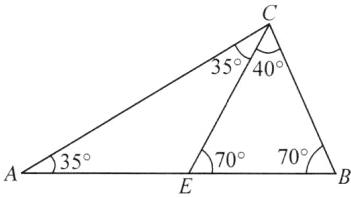
③如图所示.
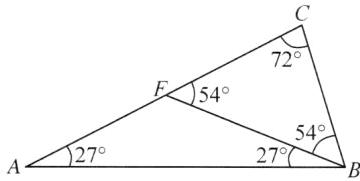
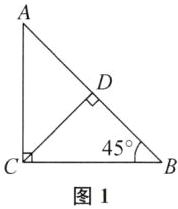
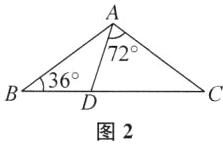
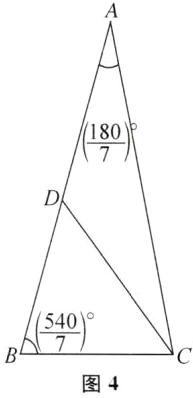
(2)$45^{\circ }$或$36^{\circ }$或$72^{\circ }$或$(\frac{540}{7})^{\circ }$ 提示:如图1、图2、图3、图4所示

(3) 两种,如图所示.


解:
(1) ①取线段 AB 的中点 D,连接 CD,则 CD 为$\triangle ABC$的“双等腰线”(图略).
②如图所示.

③如图所示.

(2)$45^{\circ }$或$36^{\circ }$或$72^{\circ }$或$(\frac{540}{7})^{\circ }$ 提示:如图1、图2、图3、图4所示




(3) 两种,如图所示.


查看更多完整答案,请扫码查看


