第34页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
9. 如图,在边长为8的正方形ABCD中,BG= BE,E,F,I,H分别为AF,AB,DF,EG的中点,求HI的长.
]
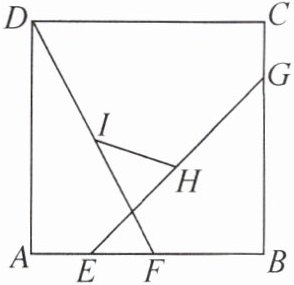
]

答案:
解:如图,以A为原点,AB,AD所在直线为x轴、y轴,建立平面直角坐标系. 根据题意,可得点D(0, 8),F(4, 0),E(2, 0),G(8, 6). 所以点I(2, 4),H(5, 3),所以HI = √((5 - 2)² + (3 - 4)²) = √10.
10. 如图1,在平面直角坐标系中,点A的坐标为(5,0),点B在第一象限内,且AB= 4,OB= 3.
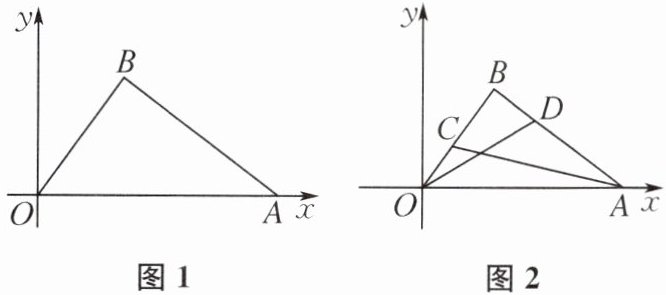
(1) 试判断△AOB的形状,并说明理由.
(2) P是线段OA上一点,且PB-PA= 1,求点P的坐标.
(3) 如图2,C,D分别为线段OB,BA上的动点,且OC= BD,求AC+OD的最小值.

(1) 试判断△AOB的形状,并说明理由.
(2) P是线段OA上一点,且PB-PA= 1,求点P的坐标.
(3) 如图2,C,D分别为线段OB,BA上的动点,且OC= BD,求AC+OD的最小值.
答案:
解:
(1)△AOB是直角三角形. 理由如下:因为点A(5, 0),所以OA = 5. 所以AB² + OB² = OA²,所以△AOB是以OA为斜边的直角三角形.
(2)过点B作BE⊥OA于点E. 设PA = x,则PB = x + 1. 因为S△AOB = 1/2OB·AB = 1/2OA·BE,所以BE = (OB·AB)/OA = 12/5. 所以OE = √(OB² - BE²) = 9/5,所以PE = |OA - OE - PA| = |16/5 - x|. 在Rt△BEP中,由勾股定理,得PB² = PE² + BE²,即(x + 1)² = (16/5 - x)² + (12/5)²,解得x = 25/14,所以OP = OA - PA = 45/14,所以点P(45/14, 0).
(3)如图,过点O作以OB为腰、∠BOH = 90°的等腰直角三角形,则HO = OB,∠HOC = ∠OBD = 90°. 连接HC. 在△HOC和△OBD中,{HO = OB,∠HOC = ∠OBD,OC = BD},所以△HOC≌△OBD,所以OD = HC,所以AC + OD = AC + HC. 当A,C,H三点共线时,AC + HC的值最小,即AC + OD取得最小值,为AH的长. 分别过点B,H作BE⊥x轴于点E,HF⊥x轴于点F. 由
(2)知,BE = 12/5,OE = 9/5. 易证△OHF≌△BOE,所以OF = BE = 12/5,HF = OE = 9/5. 所以AF = 37/5. 在Rt△AHF中,AH = √(AF² + HF²) = √58. 所以AC + OD的最小值为√58.
(1)△AOB是直角三角形. 理由如下:因为点A(5, 0),所以OA = 5. 所以AB² + OB² = OA²,所以△AOB是以OA为斜边的直角三角形.
(2)过点B作BE⊥OA于点E. 设PA = x,则PB = x + 1. 因为S△AOB = 1/2OB·AB = 1/2OA·BE,所以BE = (OB·AB)/OA = 12/5. 所以OE = √(OB² - BE²) = 9/5,所以PE = |OA - OE - PA| = |16/5 - x|. 在Rt△BEP中,由勾股定理,得PB² = PE² + BE²,即(x + 1)² = (16/5 - x)² + (12/5)²,解得x = 25/14,所以OP = OA - PA = 45/14,所以点P(45/14, 0).
(3)如图,过点O作以OB为腰、∠BOH = 90°的等腰直角三角形,则HO = OB,∠HOC = ∠OBD = 90°. 连接HC. 在△HOC和△OBD中,{HO = OB,∠HOC = ∠OBD,OC = BD},所以△HOC≌△OBD,所以OD = HC,所以AC + OD = AC + HC. 当A,C,H三点共线时,AC + HC的值最小,即AC + OD取得最小值,为AH的长. 分别过点B,H作BE⊥x轴于点E,HF⊥x轴于点F. 由
(2)知,BE = 12/5,OE = 9/5. 易证△OHF≌△BOE,所以OF = BE = 12/5,HF = OE = 9/5. 所以AF = 37/5. 在Rt△AHF中,AH = √(AF² + HF²) = √58. 所以AC + OD的最小值为√58.
11. 如图,在平面直角坐标系xOy中,点A(0,4),B为x轴正半轴上一个动点,以AB为腰作等腰直角三角形ABC,∠ABC= 90°,且点C在第一象限内.
(1) 如图1,若点B(2,0),求点C的坐标.
(2) 如图2,过点B向x轴上方作BD⊥OB,且BD= BO,在点B的运动过程中,探究点C,D之间的距离是否为定值?若为定值,求出该定值;若不是,请说明理由.
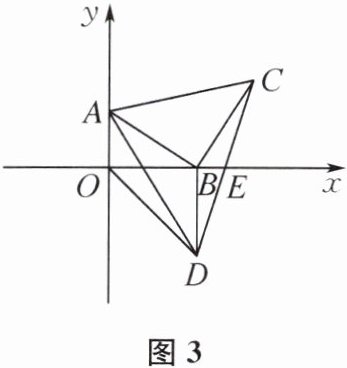
(3) 如图3,过点B向x轴下方作BD⊥OB,且BD= BO,连接CD交x轴于点E,当△ABD的面积是△BEC的面积的3倍时,求OE的长.
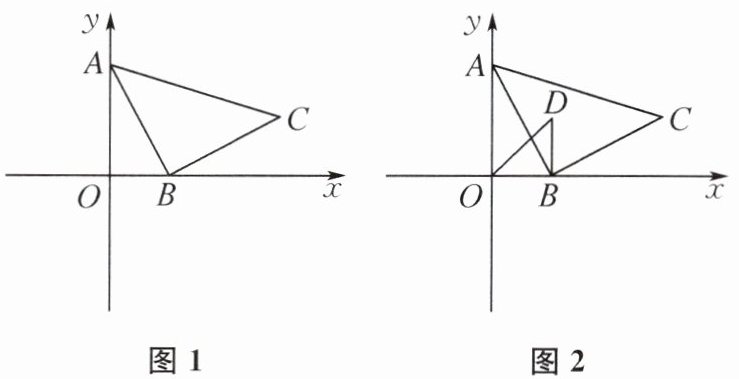
(1) 如图1,若点B(2,0),求点C的坐标.
(2) 如图2,过点B向x轴上方作BD⊥OB,且BD= BO,在点B的运动过程中,探究点C,D之间的距离是否为定值?若为定值,求出该定值;若不是,请说明理由.
(3) 如图3,过点B向x轴下方作BD⊥OB,且BD= BO,连接CD交x轴于点E,当△ABD的面积是△BEC的面积的3倍时,求OE的长.


答案:
解:
(1)因为点A(0, 4),B(2, 0),所以AO = 4,BO = 2. 过点C作CD⊥x轴于点D,可证△OAB≌△DBC(AAS),所以CD = BO = 2,BD = AO = 4,所以OD = BO + BD = 6,所以点C的坐标为(6, 2).
(2)点C,D之间的距离是为定值. 理由如下:连接CD,因为∠OBA + ∠ABD = 90°,∠DBC + ∠ABD = 90°,所以∠OBA = ∠DBC,可证△OAB≌△DCB(SAS). 所以CD = AO = 4,即点C,D之间的距离是为定值.
(3)过点C作CF⊥x轴于点F,由
(1)可知,△OAB≌△FBC,所以CF = BO,BF = AO = 4. 因为BD = BO,所以CF = BD. 可证△CFE≌△DBE,所以EF = EB = 2. 所以S△BEC = S△EFC = 1/2S△BFC = 1/2S△ABO. 由题可知S△ABD = 3S△BEC,所以S△ABD = 3/2S△ABO,所以1/2BD·BO = 3/2×1/2BO·OA,所以BD = 3/2OA = 6,所以OE = BO + EB = BD + EB = 8.
(1)因为点A(0, 4),B(2, 0),所以AO = 4,BO = 2. 过点C作CD⊥x轴于点D,可证△OAB≌△DBC(AAS),所以CD = BO = 2,BD = AO = 4,所以OD = BO + BD = 6,所以点C的坐标为(6, 2).
(2)点C,D之间的距离是为定值. 理由如下:连接CD,因为∠OBA + ∠ABD = 90°,∠DBC + ∠ABD = 90°,所以∠OBA = ∠DBC,可证△OAB≌△DCB(SAS). 所以CD = AO = 4,即点C,D之间的距离是为定值.
(3)过点C作CF⊥x轴于点F,由
(1)可知,△OAB≌△FBC,所以CF = BO,BF = AO = 4. 因为BD = BO,所以CF = BD. 可证△CFE≌△DBE,所以EF = EB = 2. 所以S△BEC = S△EFC = 1/2S△BFC = 1/2S△ABO. 由题可知S△ABD = 3S△BEC,所以S△ABD = 3/2S△ABO,所以1/2BD·BO = 3/2×1/2BO·OA,所以BD = 3/2OA = 6,所以OE = BO + EB = BD + EB = 8.
查看更多完整答案,请扫码查看


