第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
9. 在△ABC 和△A'B'C'中,AB= A'B',AC= A'C',∠C= 60°,AD,A'D'分别为边 BC,B'C'上的高,且 AD= A'D',则∠C'的度数为
60°或120°
.
答案:
60°或120° 提示:分两种情况讨论:①当∠C'为锐角时,如图1所示,因为AD,A'D'分别为边BC,B'C'上的高,所以AD⊥BC,A'D'⊥B'C',所以∠ADC=∠A'D'C'=90°,易证Rt△ADC≌Rt△A'D'C',所以∠C'=∠C=60°;②当∠A'C'B'为钝角时,如图2所示,易证Rt△ACD≌Rt△A'C'D',所以∠A'C'D'=∠C=60°,所以∠A'C'B'=120°.
10. 如图,∠ACH 是△ABC 的外角,CD 平分∠ACH,且 CD 与 BA 的延长线交于点 D,E 是线段 CD 上一动点(点 E 不与点 C,D 重合).若 EA= 2,EB= 6,令 CA+CB= n,则 n 的取值范围是
4<n<8
.
答案:
4<n<8 提示:在CH上截取CF=CA,连接EF.因为CD平分∠ACH,所以∠ACE=∠FCE.易证△ACE≌△FCE,所以EF=EA=2.在△EBF中,EB-EF<BF<EB+EF,即6-2<CF+CB<6+2,所以4<CA+CB<8,即n的取值范围是4<n<8.
11. 在探索三角形全等的条件时,老师给出了定长线段 a,b,且长度为 b 的边所对的角为 n°(0<n<90).小明和小亮按照所给条件分别画出并剪下了图1中的两个三角形,并试图把它们重合在一起(图2),其中AB= a,BD= BC= b,发现它们不全等,但他们对该图形产生了浓厚兴趣,并进行了进一步的探究.
(1) 当 n= 45 时(图2),小明测得∠ABC= 65°,请根据小明的测量结果,求∠ABD的度数.
(2) 当 n≠45 时,将△ABD 沿 AB 翻折,得到△ABD'(图3),小明和小亮发现∠D'BC 的大小与角度 n 有关,请直接写出它们的关系.
(3) 如图4,在(2)的基础上,过点 B 作 AD'的垂线,垂足为 E,延长 AE 至点 F,使得$EF= \frac{1}{2}(AD+AC)$,连接 FB,请判断△ABF 的形状,并说明理由.
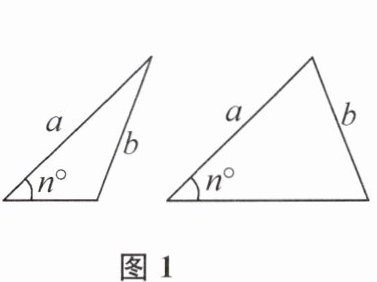
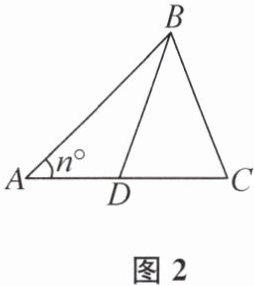
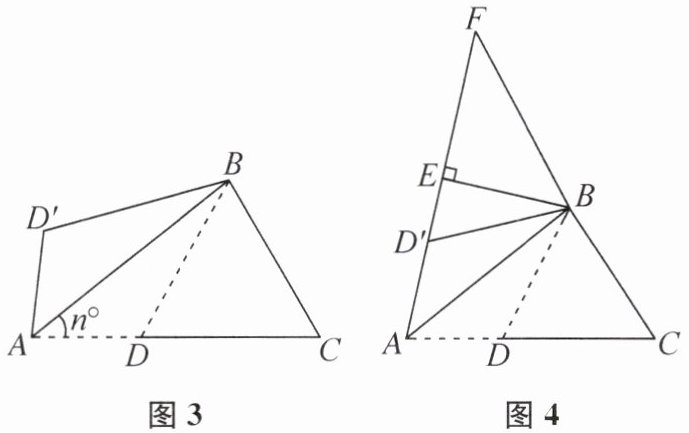
(1) 当 n= 45 时(图2),小明测得∠ABC= 65°,请根据小明的测量结果,求∠ABD的度数.
(2) 当 n≠45 时,将△ABD 沿 AB 翻折,得到△ABD'(图3),小明和小亮发现∠D'BC 的大小与角度 n 有关,请直接写出它们的关系.
(3) 如图4,在(2)的基础上,过点 B 作 AD'的垂线,垂足为 E,延长 AE 至点 F,使得$EF= \frac{1}{2}(AD+AC)$,连接 FB,请判断△ABF 的形状,并说明理由.



答案:
解:
(1)因为∠A=n°=45°,∠ABC=65°,所以∠C=180°-∠A-∠ABC=70°.因为BD=BC,所以∠BDC=∠C=70°.所以∠ABD=∠BDC-∠A=25°.
(2)∠D'BC=180°-2n°. 提示:设∠C=∠BDC=α,则∠DBC=180°-2α.因为∠ABD=∠BDC-∠DAB=α-n°,所以∠D'BC=2∠ABD+∠DBC=180°-2n°.
(3)△ABF是等腰三角形,且FB=AB.理由如下:
过点B作BT⊥AC于点T,则DT=TC.所以EF=$\frac{1}{2}(AD+AC)$=TA.根据折叠的性质,得∠D'AB=∠DAB.因为BE⊥AF,所以BE=BT.因为∠BEF=∠BTA=90°,所以△FBE≌△ABT(SAS),所以FB=AB,所以△ABF是等腰三角形.
(1)因为∠A=n°=45°,∠ABC=65°,所以∠C=180°-∠A-∠ABC=70°.因为BD=BC,所以∠BDC=∠C=70°.所以∠ABD=∠BDC-∠A=25°.
(2)∠D'BC=180°-2n°. 提示:设∠C=∠BDC=α,则∠DBC=180°-2α.因为∠ABD=∠BDC-∠DAB=α-n°,所以∠D'BC=2∠ABD+∠DBC=180°-2n°.
(3)△ABF是等腰三角形,且FB=AB.理由如下:
过点B作BT⊥AC于点T,则DT=TC.所以EF=$\frac{1}{2}(AD+AC)$=TA.根据折叠的性质,得∠D'AB=∠DAB.因为BE⊥AF,所以BE=BT.因为∠BEF=∠BTA=90°,所以△FBE≌△ABT(SAS),所以FB=AB,所以△ABF是等腰三角形.
12. 在△ABC 和△DCE 中,CA= CB,CD= CE,∠CAB= ∠CBA= ∠CDE= ∠CED= α.
(1) 如图1,延长 AD,EB,相交于点 O.
①求证:BE= AD;
②用含 α 的式子表示∠AOB 的度数:
(2) 如图2,当 α= 45°时,连接 BD,AE,作 CM⊥AE 于点 M,延长 MC 与 BD 交于点 N,求证:N 是 BD 的中点.
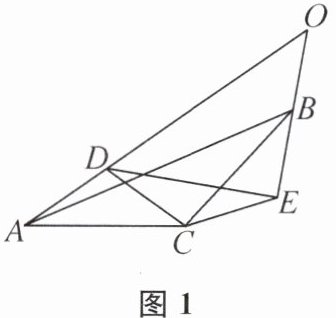
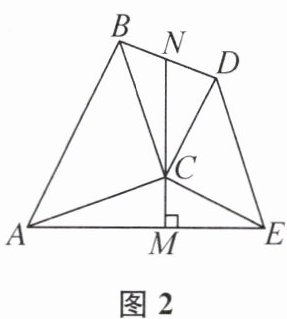
(1) 如图1,延长 AD,EB,相交于点 O.
①求证:BE= AD;
②用含 α 的式子表示∠AOB 的度数:
2α
.(2) 如图2,当 α= 45°时,连接 BD,AE,作 CM⊥AE 于点 M,延长 MC 与 BD 交于点 N,求证:N 是 BD 的中点.


(1)①证明:因为CA=CB,CD=CE,∠CAB=∠CBA=∠CDE=∠CED=α,所以∠ACB=180°-2α,∠DCE=180°-2α,所以∠ACB=∠DCE.所以∠ACB-∠DCB=∠DCE-∠DCB,所以∠ACD=∠BCE.在△ACD和△BCE中,$\left\{\begin{array}{l}CA=CB,\\ ∠ACD=∠BCE,\\ CD=CE,\end{array}\right.$所以△ACD≌△BCE,所以BE=AD.
(2)证明:过点B作BP⊥MN,交MN的延长线于点P,过点D作DQ⊥MN于点Q.因为α=45°,所以∠ACB=∠DCE=90°,所以∠BCP=90°-∠ACM=∠CAM.在△CBP和△ACM中,$\left\{\begin{array}{l}∠BPC=∠CMA,\\ ∠BCP=∠CAM,\\ CB=AC,\end{array}\right.$所以△CBP≌△ACM,所以MC=PB.同理,MC=QD,所以QD=PB.在△BPN和△DQN中,$\left\{\begin{array}{l}∠BNP=∠DNQ,\\ ∠BPN=∠DQN,\\ BP=DQ,\end{array}\right.$所以△BPN≌△DQN,所以BN=DN,即N是BD的中点.
(2)证明:过点B作BP⊥MN,交MN的延长线于点P,过点D作DQ⊥MN于点Q.因为α=45°,所以∠ACB=∠DCE=90°,所以∠BCP=90°-∠ACM=∠CAM.在△CBP和△ACM中,$\left\{\begin{array}{l}∠BPC=∠CMA,\\ ∠BCP=∠CAM,\\ CB=AC,\end{array}\right.$所以△CBP≌△ACM,所以MC=PB.同理,MC=QD,所以QD=PB.在△BPN和△DQN中,$\left\{\begin{array}{l}∠BNP=∠DNQ,\\ ∠BPN=∠DQN,\\ BP=DQ,\end{array}\right.$所以△BPN≌△DQN,所以BN=DN,即N是BD的中点.
答案:
(1)①证明:因为CA=CB,CD=CE,∠CAB=∠CBA=∠CDE=∠CED=α,所以∠ACB=180°-2α,∠DCE=180°-2α,所以∠ACB=∠DCE.所以∠ACB-∠DCB=∠DCE-∠DCB,所以∠ACD=∠BCE.在△ACD和△BCE中,$\left\{\begin{array}{l}CA=CB,\\ ∠ACD=∠BCE,\\ CD=CE,\end{array}\right.$所以△ACD≌△BCE,所以BE=AD.
② 2α 提示:因为△ACD≌△BCE,所以∠CAD=∠CBE=α+∠BAO.因为∠ABE=∠AOB+∠BAO,所以∠CBE+α=∠AOB+∠BAO,所以∠BAO+α+α=∠AOB+∠BAO,所以∠AOB=2α.
(2)证明:过点B作BP⊥MN,交MN的延长线于点P,过点D作DQ⊥MN于点Q.因为α=45°,所以∠ACB=∠DCE=90°,所以∠BCP=90°-∠ACM=∠CAM.在△CBP和△ACM中,$\left\{\begin{array}{l}∠BPC=∠CMA,\\ ∠BCP=∠CAM,\\ CB=AC,\end{array}\right.$所以△CBP≌△ACM,所以MC=PB.同理,MC=QD,所以QD=PB.在△BPN和△DQN中,$\left\{\begin{array}{l}∠BNP=∠DNQ,\\ ∠BPN=∠DQN,\\ BP=DQ,\end{array}\right.$所以△BPN≌△DQN,所以BN=DN,即N是BD的中点.
(1)①证明:因为CA=CB,CD=CE,∠CAB=∠CBA=∠CDE=∠CED=α,所以∠ACB=180°-2α,∠DCE=180°-2α,所以∠ACB=∠DCE.所以∠ACB-∠DCB=∠DCE-∠DCB,所以∠ACD=∠BCE.在△ACD和△BCE中,$\left\{\begin{array}{l}CA=CB,\\ ∠ACD=∠BCE,\\ CD=CE,\end{array}\right.$所以△ACD≌△BCE,所以BE=AD.
② 2α 提示:因为△ACD≌△BCE,所以∠CAD=∠CBE=α+∠BAO.因为∠ABE=∠AOB+∠BAO,所以∠CBE+α=∠AOB+∠BAO,所以∠BAO+α+α=∠AOB+∠BAO,所以∠AOB=2α.
(2)证明:过点B作BP⊥MN,交MN的延长线于点P,过点D作DQ⊥MN于点Q.因为α=45°,所以∠ACB=∠DCE=90°,所以∠BCP=90°-∠ACM=∠CAM.在△CBP和△ACM中,$\left\{\begin{array}{l}∠BPC=∠CMA,\\ ∠BCP=∠CAM,\\ CB=AC,\end{array}\right.$所以△CBP≌△ACM,所以MC=PB.同理,MC=QD,所以QD=PB.在△BPN和△DQN中,$\left\{\begin{array}{l}∠BNP=∠DNQ,\\ ∠BPN=∠DQN,\\ BP=DQ,\end{array}\right.$所以△BPN≌△DQN,所以BN=DN,即N是BD的中点.
查看更多完整答案,请扫码查看


