第17页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 下列叙述中,正确的是 (
A.a 的平方根是$\sqrt{a}$
B.$(-a)^{2}的平方根是-a$
C.一个数总有两个平方根
D.$-a是a^{2}$的一个平方根
D
)A.a 的平方根是$\sqrt{a}$
B.$(-a)^{2}的平方根是-a$
C.一个数总有两个平方根
D.$-a是a^{2}$的一个平方根
答案:
D
2. 若$a^{2}+b^{2}= 15$,$ab= 6$,则$a-b$的值为 (
A.$-\sqrt{3}$
B.$\sqrt{3}$
C.$\pm\sqrt{3}$
D.$\pm3$
C
)A.$-\sqrt{3}$
B.$\sqrt{3}$
C.$\pm\sqrt{3}$
D.$\pm3$
答案:
C
3. (2024·德阳市中考)将一组数$\sqrt{2},2,\sqrt{6},\sqrt{8},\sqrt{10},\sqrt{12},…,\sqrt{2n},…$按以下方式进行排列,则第八行左起第1个数是(
第一行 $\sqrt{2}$
第二行 2 $\sqrt{6}$
第三行 $\sqrt{8}$ $\sqrt{10}$ $\sqrt{12}$
……

A.$\sqrt{54}$
B.$\sqrt{56}$
C.$\sqrt{58}$
D.$\sqrt{60}$
C
)第一行 $\sqrt{2}$
第二行 2 $\sqrt{6}$
第三行 $\sqrt{8}$ $\sqrt{10}$ $\sqrt{12}$
……

A.$\sqrt{54}$
B.$\sqrt{56}$
C.$\sqrt{58}$
D.$\sqrt{60}$
答案:
C
4. 交通事故统计发现,每年的汽车追尾事故占所有事故的30%左右.造成追尾事故的主要原因是刹车距离把握不当.研究发现,在柏油路面上,刹车距离s与车速v的关系式是$s= \frac{v^{2}}{2g\mu}$(其中$g= 10$,$\mu=0.9$),当刹车距离增加一倍时,车速变为原来的(
A.1倍
B.$\sqrt{2}$倍
C.$(\sqrt{2}-1)$倍
D.2倍
B
)A.1倍
B.$\sqrt{2}$倍
C.$(\sqrt{2}-1)$倍
D.2倍
答案:
B 提示:由题意知,$s=\frac{v^{2}}{18}$,当刹车距离增加一倍时,$2s=\frac{(\sqrt{2}v)^{2}}{18}$,即车速变为原来的$\sqrt{2}$倍.
5. 设$S_{1}= 1+\frac{1}{1^{2}}+\frac{1}{2^{2}}$,$S_{2}= 1+\frac{1}{2^{2}}+\frac{1}{3^{2}}$,$S_{3}= 1+\frac{1}{3^{2}}+\frac{1}{4^{2}}$,…,$S_{n}= 1+\frac{1}{n^{2}}+\frac{1}{(n+1)^{2}}$,则$\sqrt{S_{1}}+\sqrt{S_{2}}+\sqrt{S_{3}}+…+\sqrt{S_{24}}$的值为 (
A.$\frac{24}{25}$
B.$\frac{\sqrt{24}}{5}$
C.$24\frac{24}{25}$
D.$23\frac{23}{24}$
C
)A.$\frac{24}{25}$
B.$\frac{\sqrt{24}}{5}$
C.$24\frac{24}{25}$
D.$23\frac{23}{24}$
答案:
C 提示:因为$\sqrt{S_{1}}=\sqrt{1+1+\frac{1}{4}}=\frac{3}{2}=1+1-\frac{1}{2}$,$\sqrt{S_{2}}=\sqrt{1+\frac{1}{4}+\frac{1}{9}}=\frac{7}{6}=1+\frac{1}{2}-\frac{1}{3}$,$\sqrt{S_{3}}=\sqrt{1+\frac{1}{9}+\frac{1}{16}}=\frac{13}{12}=1+\frac{1}{3}-\frac{1}{4}$,$\sqrt{S_{4}}=\sqrt{1+\frac{1}{16}+\frac{1}{25}}=\frac{21}{20}=1+\frac{1}{4}-\frac{1}{5}$,…,所以可推知$\sqrt{S_{n}}=1+\frac{1}{n}-\frac{1}{n+1}$,所以$\sqrt{S_{1}}+\sqrt{S_{2}}+\cdots+\sqrt{S_{24}}=1+1-\frac{1}{2}+1+\frac{1}{2}-\frac{1}{3}+\cdots+1+\frac{1}{24}-\frac{1}{25}=24\frac{24}{25}$.
6. (2024 淮安市校级期中)已知某正数的两个平方根分别是$m+4和2m-16$,则$m= $
4
.
答案:
4
7. 若三个互不相等的负整数,两两乘积的算术平方根都是整数,则称这三个数为“完美组合数”.例如:$-9$,$-4$,$-1$这三个数,$\sqrt{(-9)×(-4)}= 6$,$\sqrt{(-9)×(-1)}= 3$,$\sqrt{(-4)×(-1)}= 2$,其结果6,3,2都是整数,所以$-1$,$-4$,$-9$这三个数称为“完美组合数”.若三个数$-3$,$m$,$-12$是“完美组合数”,其中有两个数乘积的算术平方根为12,则$m=$
-48
.
答案:
-48
8. 若奇数$x$,$y满足y= \sqrt{x-24}-\sqrt{26-x}+11$,则$x+y$的平方根为
±6
.
答案:
±6 提示:根据题意,得$\left\{\begin{array}{l} x-24\geq0,\\ 26-x\geq0,\end{array}\right.$解得24≤x≤26.因为x是奇数,所以x=25,此时y=11.所以x+y的平方根为±6.
9. 计算①$\sqrt{1^{3}}$,②$\sqrt{1^{3}+2^{3}}$,③$\sqrt{1^{3}+2^{3}+3^{3}}$,④$\sqrt{1^{3}+2^{3}+3^{3}+4^{3}}$的结果,用你发现的规律直接写出下面式子的值:$\sqrt{1^{3}+2^{3}+3^{3}+…+28^{3}}= $
406
.
答案:
406 提示:根据题意,得$\sqrt{1^{3}}=1$,$\sqrt{1^{3}+2^{3}}=1+2$,$\sqrt{1^{3}+2^{3}+3^{3}}=1+2+3$,$\sqrt{1^{3}+2^{3}+3^{3}+4^{3}}=1+2+3+4$,…,依次类推,$\sqrt{1^{3}+2^{3}+3^{3}+\cdots+28^{3}}=1+2+3+\cdots+28=406$.
10. 给出表格:
| a | 0.0001 | 0.01 | 1 | 100 | 10000 |
| $\sqrt{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |
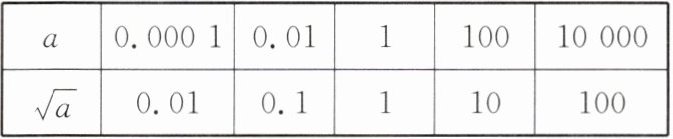
利用表格中的规律计算:已知$\sqrt{15}= k$,$\sqrt{0.15}= a$,$\sqrt{1500}= b$,则$a+b= $______(用含$k$的代数式表示).
| a | 0.0001 | 0.01 | 1 | 100 | 10000 |
| $\sqrt{a}$ | 0.01 | 0.1 | 1 | 10 | 100 |

利用表格中的规律计算:已知$\sqrt{15}= k$,$\sqrt{0.15}= a$,$\sqrt{1500}= b$,则$a+b= $______(用含$k$的代数式表示).
10.1k
答案:
10.1k 提示:由题意,得a=0.1k,b=10k,则a+b=10.1k.
11. 已知$a$,$b$,$c满足|2a-4|+|b+2|+\sqrt{(a-3)b^{2}}+a^{2}+c^{2}= 2+2ac$,求$a-b+c$的值.
答案:
解:原式可化为$|2a-4|+|b+2|+\sqrt{(a-3)b^{2}}+(a-c)^{2}=2$.①当b=0时,$|2a-4|+(a-c)^{2}=0$,所以a=2,c=2,a-b+c=4;②当$b^{2}>0$时,由$\sqrt{(a-3)b^{2}}$有意义,可得a≥3,故|2a-4|-2=|2a-4-2|,$|2a-4-2|+|b+2|+\sqrt{(a-3)b^{2}}+(a-c)^{2}=0$,则a=3=c,b=-2,所以a-b+c=8.综上所述,a-b+c的值为4或8.
查看更多完整答案,请扫码查看


