《2025年小题狂做八年级数学上册苏科版巅峰版》

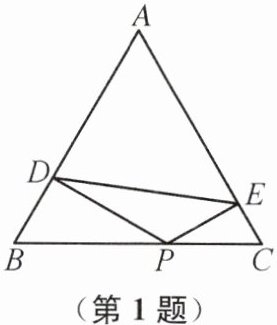
1. 如图,△ABC 是等边三角形,P 是边 BC 上任意一点,PD⊥AB,PE⊥AC,连接 DE. 记△ADE 的周长为 $ l_1 $,四边形 BDEC 的周长为 $ l_2 $,则 $ l_1 $ 与 $ l_2 $ 的大小关系是 (A)

A.$ l_1 = l_2 $
B.$ l_1 ＞ l_2 $
C.$ l_2 ＞ l_1 $
D.无法确定
]

答案： A　提示:因为△ABC是等边三角形,所以AB=AC=BC,∠B=∠C=60°,所以∠BPD=∠CPE=30°.所以在Rt△BDP和Rt△CEP中,BP=2BD,CP=2CE,所以BD+CE= $\frac{1}{2}$BC,所以BD+CE+BC= $\frac{3}{2}$BC,$l_2$= $\frac{3}{2}$BC+DE.因为AD+AE=AB+AC-BD-CE=AB+AC- $\frac{1}{2}$BC= $\frac{3}{2}$BC,所以$l_1$= $\frac{3}{2}$BC+DE.所以$l_1$= $l_2$.

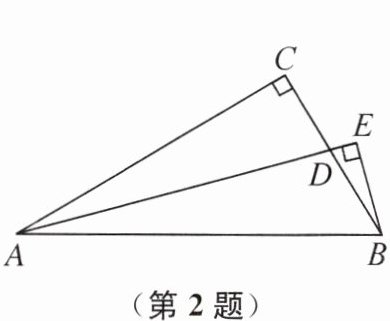
2. 如图,在 Rt△ABC 中,∠ACB= 90°,∠ABC= 2∠BAC,AD 平分∠BAC 交 BC 于点 D,BE⊥AD,交 AD 的延长线于点 E. 若 AB= 12,则△ABE 的面积是 ( )

A.18
B.36
C.$ 9\sqrt{3} $
D.$ 18\sqrt{3} $
]

答案：
A　提示:如图,延长BE交AC的延长线于点F.因为∠ACB=90°,∠ABC=2∠BAC,所以∠BAC=30°,所以BC= $\frac{1}{2}$AB=6.因为AD平分∠BAC,BE⊥AD,所以易证△AEF≌△AEB(ASA),所以AF=AB=12,所以$S_{\triangle ABF}$= $\frac{1}{2}$AF·BC=36,所以$S_{\triangle ABE}$= $\frac{1}{2}$$S_{\triangle ABF}$=18.
　　　　　

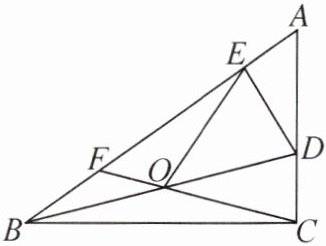
3. 如图,在△ABC 中,∠BCA= 90°,D 为边 AC 上一动点,O 为 BD 的中点,DE⊥AB,垂足为 E,连接 OE,CO,延长 CO 交 AB 于点 F,设∠BAC= α,则 (B)

A.∠EOF= $ \frac{3}{2}\alpha $
B.∠EOF= 2α
C.∠EOF= 180°-α
D.∠EOF= 180°-2α
]

答案： B　提示:设∠ABD=β,则∠ODC=∠A+∠ABD=α+β.因为DE⊥AB,所以∠BED=90°,所以∠BDE=90°-β.因为O为BD的中点,所以OE= $\frac{1}{2}$BD=OD,所以∠OED=∠ODE=90°-β.同理,得OC=OD,所以∠OCD=∠ODC=α+β.所以∠EOD=180°-2(90°-β)=2β,∠COD=180°-2(α+β)=180°-2α-2β.所以∠EOF=180°-∠EOD-∠COD=180°-2β-(180°-2α-2β)=2α.

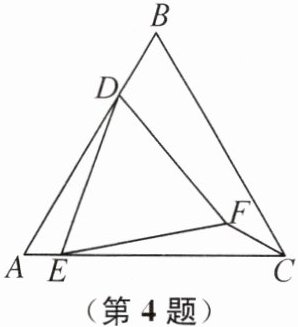
4. 如图,在等边三角形 ABC 中,D,E 分别为边 AB,AC 上的动点,BD= 2AE,连接 DE,以 DE 为边在△ABC 内作等边三角形 DEF,连接 CF. 当点 D 从点 A 向点 B 运动(不运动到点 B)时,∠ECF 的大小变化情况是 (A)

A.不变
B.变小
C.变大
D.先变大后变小
]

答案： A　提示:在AC上截取CN=AE,连接FN.因为AD=AB-BD,NE=AC-AE-CN=AC-2AE,BD=2AE,所以AD=NE.因为∠ADE=∠DEN-∠A=∠DEF+∠NEF-∠A=∠NEF,所以易证△ADE≌△NEF(SAS),所以AE=NF,∠FNE=∠A=60°.所以NF=CN,所以∠NCF=∠NFC.因为∠FNE=∠NCF+∠NFC=60°,所以∠NCF=30°,即∠ECF=30°,即∠ECF的大小不变.

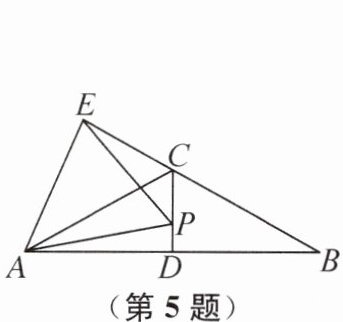
5. 如图,在△ABC 中,AC= BC,∠B= 30°,D 为 AB 的中点,P 为线段 CD 上一点,E 为 BC 的延长线上一点,且 PA= PE. 有下列结论：①∠PAD+∠PEC= 30°；②△PAE 为等边三角形；③PD= CE-CP；④$ S_{四边形AECP}= S_{\triangle ABC} $. 其中正确的结论是 ( C )

A.①②③④
B.①②
C.①②④
D.③④
]

答案： C　提示:连接BP.因为AC=BC,∠ABC=30°,D是AB的中点,所以∠CAB=∠ABC=30°,AD=BD,CD⊥AB,所以CD是AB的垂直平分线,所以PA=PB,又因为PA=PE,所以PA=PB=PE,所以∠PAD=∠PBA,∠PEB=∠PBE,所以∠PAD+∠PEC=∠PBA+∠PBE=∠ABC=30°,故①正确;因为PA=PE,所以∠PAE=∠PEA,因为∠ABC=∠PAD+∠PEC=30°,所以∠PAE+∠PEA=180°-∠ABC-∠PAD-∠PEC=120°,所以∠APE=60°,所以△PAE是等边三角形,故②正确;延长PD至点P',使P'D=PD,连接AP',则AP=AP',∠PAD=∠P'AD,因为△PAE是等边三角形,所以AE=AP,所以AE=AP',因为∠CAD=∠CAP+∠PAD=30°,所以2∠CAP+2∠PAD=60°,所以∠CAP+∠PAD+∠P'AD=60°-∠CAP,即∠P'AC=∠EAC,因为AC=AC,所以△P'AC≌△EAC,所以CE=CP'=CP+PD+P'D=CP+2PD,所以PD= $\frac{CE-CP}{2}$,故③错误;过点A作AF⊥BE于点F,在CB上截取CG=CP,连接PG,因为CG=CP,∠BCD=60°,所以△CPG是等边三角形,所以∠CGP=∠PCG=60°,所以∠ECP=∠BGP=120°,且PE=PB,∠PEB=∠PBE,所以△PCE≌△PGB,所以CE=GB,所以AC=BC=GB+CG=CE+CP,因为∠ABC=30°,AF⊥BE,所以AF= $\frac{1}{2}$AB=AD,所以$S_{四边形AECP}$= $\frac{1}{2}$CE·AF+ $\frac{1}{2}$CP·AD=$S_{\triangle ABC}$,故④正确.

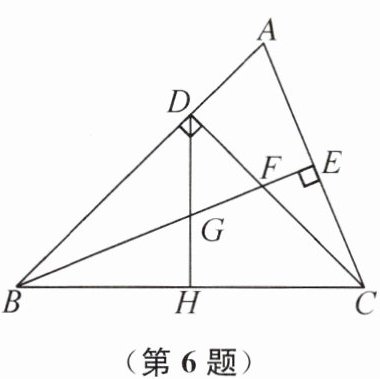
6. (2024 南京市校级期中)如图,在△ABC 中,∠ABC= 45°,CD⊥AB 于点 D,BE 平分∠ABC,且 BE⊥AC 于点 E,与 CD 相交于点 F,H 是边 BC 的中点,连接 DH 与 BE 相交于点 G. 给出下列结论：①BF= AC；②CE= $ \frac{1}{2}BF $；③DG= FG；④BD+DF= BC. 其中正确的有______(填序号).
]

①②④

答案： ①②④　提示:因为CD⊥AB,BE⊥AC,所以∠BDC=∠ADC=∠AEB=90°,所以∠A=∠DFB,因为∠ABC=45°,所以△BDC为等腰直角三角形,所以BD=CD,所以△BDF≌△CDA(AAS),所以BF=AC,故①正确;因为BE平分∠ABC,且BE⊥AC于点E,所以∠ABE=∠CBE,∠AEB=∠CEB=90°,所以△ABE≌△CBE(ASA),所以AE=CE= $\frac{1}{2}$AC,因为BF=AC,所以CE= $\frac{1}{2}$BF,故②正确;因为∠DBG= $\frac{1}{2}$∠ABC=22.5°,∠BDG= $\frac{1}{2}$∠BDC=45°,所以∠DGF=67.5°,∠DFG=90°-∠DBG=67.5°,所以∠DGF=∠DFG=67.5°,所以DG=DF,因为∠GDF= $\frac{1}{2}$∠BDC=45°,所以DG≠GF,故③错误;因为△BDF≌△CDA,所以DF=DA,所以BD+DF=BD+DA=AB,因为△ABE≌△CBE,所以AB=CB,所以BD+DF=BC,故④正确.

7. 如图,在△ABC 中,AB= AC,BD 平分∠ABC 交 AC 于点 D,点 E 在 BA 的延长线上,DB= DE. 若 BC= 7,AE= 2,则线段 AD 的长为______5.

答案： 5　提示:在BC上截取BF=AE,连接DF.因为DB=DE,所以∠E=∠DBE.因为BD平分∠ABC,所以∠ABD=∠DBF,所以∠E=∠DBF,所以△DEA≌△DBF(SAS),所以DF=DA,∠EAD=∠BFD,所以∠BAC=∠CFD.因为AB=AC,所以∠ABC=∠C,所以∠CDF=∠ABC=∠C,所以CF=DF,所以AD=CF.因为BC=7,AE=2,所以AD=CF=BC-BF=5.