第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
4. [模型观念;应用意识]如图1,一辆货车从南京出发匀速驶往上海,途经苏州;同时,一辆轿车从苏州出发匀速驶往南京,到达南京后停留1h,然后原速返回苏州,两车同时到达目的地. 设货车行驶xh时,货车与苏州的距离为$y_1km,$轿车与苏州的距离为$y_2km,y_1,y_2$与x之间的函数图象如图2所示.
(1)货车的速度是______km/h,轿车的速度是______km/h.
(2)通过计算,分别解释点G,H的实际意义.
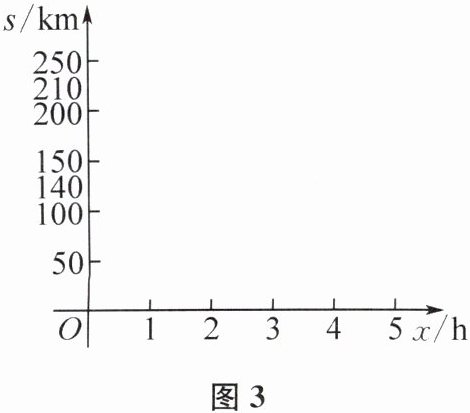
(3)设轿车、货车之间的距离为skm,在图3中画出s与x之间的函数图象(标明必要的数据).

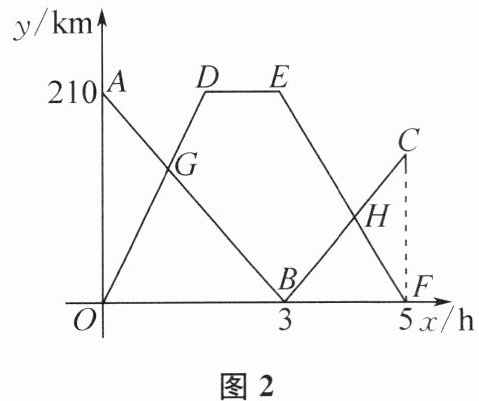
(1)货车的速度是______km/h,轿车的速度是______km/h.
(2)通过计算,分别解释点G,H的实际意义.
(3)设轿车、货车之间的距离为skm,在图3中画出s与x之间的函数图象(标明必要的数据).



答案:
解:
(1)70 105
(2)设AB所在直线的函数表达式为y=kx + b(k≠0),将点(0,210),(3,0)代入,解得k = - 70,b = 210,所以AB所在直线的函数表达式为y = - 70x + 210(0≤x≤3).因为货车的速度为70km/h,易求BC所在直线的函数表达式为y = 70(x - 3)=70x - 210(3<x≤5).因为轿车的速度为105km/h,所以$\frac{210}{105}$ = 2(h),所以点D(2,210),E(3,210),易求OD所在直线的函数表达式为y = 105x(0≤x≤2).由待定系数法,易求EF所在直线的函数表达式为y = - 105x + 525(3≤x≤5).由$\begin{cases}y = - 70x + 210\\y = 105x\end{cases}$得$\begin{cases}x = 1.2\\y = 126\end{cases}$,所以点G(1.2,126);由$\begin{cases}y = 70x - 210\\y = - 105x + 525\end{cases}$得$\begin{cases}x = 4.2\\y = 84\end{cases}$,所以点H(4.2,84).所以点G的实际意义为轿车与货车出发1.2h时,在距离苏州126km的地方第一次相遇;点H的实际意义为轿车与货车出发4.2h时,货车已经经过苏州,轿车在返回苏州的路上,且都距离苏州84km.
(3)s与x之间的函数图象如图所示.
提示:由题意可知,南京到苏州的距离为210km,苏州到上海的距离为2×70 = 140(km).当0≤x≤1.2时,s = - 175x + 210,0≤s≤210;当1.2<x≤2时,s = 175x - 210,0<s≤140;当x = 2时,轿车到达南京,停留1h;当2<x≤3时,s = 70x,140<s≤210;当x = 3时,轿车开始从南京返回,货车到达苏州;当3<x≤5时,s = - 35x + 315,140≤s<210.

解:
(1)70 105
(2)设AB所在直线的函数表达式为y=kx + b(k≠0),将点(0,210),(3,0)代入,解得k = - 70,b = 210,所以AB所在直线的函数表达式为y = - 70x + 210(0≤x≤3).因为货车的速度为70km/h,易求BC所在直线的函数表达式为y = 70(x - 3)=70x - 210(3<x≤5).因为轿车的速度为105km/h,所以$\frac{210}{105}$ = 2(h),所以点D(2,210),E(3,210),易求OD所在直线的函数表达式为y = 105x(0≤x≤2).由待定系数法,易求EF所在直线的函数表达式为y = - 105x + 525(3≤x≤5).由$\begin{cases}y = - 70x + 210\\y = 105x\end{cases}$得$\begin{cases}x = 1.2\\y = 126\end{cases}$,所以点G(1.2,126);由$\begin{cases}y = 70x - 210\\y = - 105x + 525\end{cases}$得$\begin{cases}x = 4.2\\y = 84\end{cases}$,所以点H(4.2,84).所以点G的实际意义为轿车与货车出发1.2h时,在距离苏州126km的地方第一次相遇;点H的实际意义为轿车与货车出发4.2h时,货车已经经过苏州,轿车在返回苏州的路上,且都距离苏州84km.
(3)s与x之间的函数图象如图所示.
提示:由题意可知,南京到苏州的距离为210km,苏州到上海的距离为2×70 = 140(km).当0≤x≤1.2时,s = - 175x + 210,0≤s≤210;当1.2<x≤2时,s = 175x - 210,0<s≤140;当x = 2时,轿车到达南京,停留1h;当2<x≤3时,s = 70x,140<s≤210;当x = 3时,轿车开始从南京返回,货车到达苏州;当3<x≤5时,s = - 35x + 315,140≤s<210.

5. [创新意识;推理能力]
【问题】我们已经研究了等腰三角形的一些基本性质,如“等边对等角”“三线合一”等. 对于一般三角形,有哪些对应的性质呢?
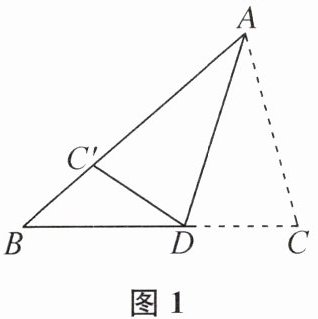
(1)【探索1】小华猜想:在△ABC中,如果AB>AC,那么∠C>∠B. 也就是说:三角形中较大的边所对的角也比较大(简称“大边对大角”). 如图1,小华把AC沿∠A的平分线AD翻折,使点C落在AB上的点C'处,从而得到证明思路. 请根据这个思路,结合图1写出证明过程.
(2)【探索2】小华通过画图发现:若AM,AD,AH分别是△ABC的中线、角平分线和高,且AB≠AC,则点D在直线BC上的位置始终处于点M和点H之间. 你认为这个结论是否一定成立?如果成立,不妨设AB>AC,请结合图2进行证明;如果不成立,请举出反例.

【问题】我们已经研究了等腰三角形的一些基本性质,如“等边对等角”“三线合一”等. 对于一般三角形,有哪些对应的性质呢?
(1)【探索1】小华猜想:在△ABC中,如果AB>AC,那么∠C>∠B. 也就是说:三角形中较大的边所对的角也比较大(简称“大边对大角”). 如图1,小华把AC沿∠A的平分线AD翻折,使点C落在AB上的点C'处,从而得到证明思路. 请根据这个思路,结合图1写出证明过程.
(2)【探索2】小华通过画图发现:若AM,AD,AH分别是△ABC的中线、角平分线和高,且AB≠AC,则点D在直线BC上的位置始终处于点M和点H之间. 你认为这个结论是否一定成立?如果成立,不妨设AB>AC,请结合图2进行证明;如果不成立,请举出反例.


答案:
证明:
(1)由翻折的性质,得∠AC'D = ∠C.因为∠AC'D是△BC'D的一个外角,所以∠AC'D = ∠B + ∠BDC',即∠AC'D>∠B,所以∠C>∠B.
(2)这个结论一定成立,理由如下:
延长AM至点E,使EM = AM,连接BE.因为AM是△ABC的中线,所以CM = BM.在△ACM和△EBM中,$\begin{cases}AM = EM\\∠AMC = ∠EMB\\CM = BM\end{cases}$,所以△ACM≌△EBM,所以∠CAM = ∠E,AC = EB.因为AB>AC,所以AB>EB,所以∠E>∠BAM,所以∠E + ∠BAM>2∠BAM.因为AD平分∠BAC,所以∠BAC = 2∠BAD.因为∠E + ∠BAM = ∠CAM + ∠BAM = ∠BAC = 2∠BAD,所以2∠BAD>2∠BAM,即∠BAD>∠BAM.因为AH是△ABC的高,所以AH⊥BC,所以∠AHB = ∠AHC = 90°,所以∠BAH = 90° - ∠ABC,∠CAH = 90° - ∠ACB.因为AB>AC,所以∠ACB>∠ABC,所以∠BAH>∠CAH.所以∠BAH + ∠BAH>∠CAH + ∠BAH,即2∠BAH>∠BAC.所以2∠BAH>2∠BAD,即∠BAH>∠BAD.所以∠BAH>∠BAD>∠BAM.所以点D在点M与点H之间.(特别提醒:要证明点D在直线BC上的位置始终处于点M和点H之间,只需证明∠BAH>∠BAD>∠BAM即可)
(1)由翻折的性质,得∠AC'D = ∠C.因为∠AC'D是△BC'D的一个外角,所以∠AC'D = ∠B + ∠BDC',即∠AC'D>∠B,所以∠C>∠B.
(2)这个结论一定成立,理由如下:
延长AM至点E,使EM = AM,连接BE.因为AM是△ABC的中线,所以CM = BM.在△ACM和△EBM中,$\begin{cases}AM = EM\\∠AMC = ∠EMB\\CM = BM\end{cases}$,所以△ACM≌△EBM,所以∠CAM = ∠E,AC = EB.因为AB>AC,所以AB>EB,所以∠E>∠BAM,所以∠E + ∠BAM>2∠BAM.因为AD平分∠BAC,所以∠BAC = 2∠BAD.因为∠E + ∠BAM = ∠CAM + ∠BAM = ∠BAC = 2∠BAD,所以2∠BAD>2∠BAM,即∠BAD>∠BAM.因为AH是△ABC的高,所以AH⊥BC,所以∠AHB = ∠AHC = 90°,所以∠BAH = 90° - ∠ABC,∠CAH = 90° - ∠ACB.因为AB>AC,所以∠ACB>∠ABC,所以∠BAH>∠CAH.所以∠BAH + ∠BAH>∠CAH + ∠BAH,即2∠BAH>∠BAC.所以2∠BAH>2∠BAD,即∠BAH>∠BAD.所以∠BAH>∠BAD>∠BAM.所以点D在点M与点H之间.(特别提醒:要证明点D在直线BC上的位置始终处于点M和点H之间,只需证明∠BAH>∠BAD>∠BAM即可)
查看更多完整答案,请扫码查看


