《2025年小题狂做八年级数学上册苏科版巅峰版》

1. (2025 南京市玄武区期末)如图是某游乐场每天的利润 y(万元)(票价总收入减去运营成本)与每天售出的门票张数 x(张)的函数图象.目前该游乐场亏损,为了扭亏,游乐场同时采取降低运营成本、提高票价两种措施.下列图象中能表示采取措施后的图象是 (A)

答案： A

2. 某中学组织八年级学生前往A城参加研学活动,学生分为甲、乙两队相继从学校乘车出发,沿同一路线匀速前往A城.甲、乙两队离开学校的距离y(km)与甲队行驶的时间t(h)之间的函数关系如图所示,有下列结论:①学校与A城相距300 km;②乙队比甲队晚出发1 h,却早到1 h;③乙队出发后2.5 h追上甲队;④甲、乙两队相距50 km时,$t= \frac {5}{4}或t= \frac {5}{6}$.其中正确的结论有 (C)

A.0个
B.1个
C.2个
D.3个

答案： C　　提示:由图象可得，学校与A城相距300km，故①正确.乙队比甲队晚出发1h，却早到1h，故②正确.甲的速度为300÷5=60(km/h)，乙的速度为300÷(4−1)=100(km/h).设乙队出发后a h追上甲队，则100a = 60(a + 1)，得a = 1.5，故③错误.当甲、乙两队相距50km时，分四种情况，乙出发前，此时t = 50÷60 = $\frac{5}{6}$；乙出发后到甲、乙相遇前，此时60t−50 = 100(t−1)，得t = $\frac{5}{4}$；甲、乙相遇之后到乙到达目的地前，此时60t + 50 = 100(t−1)，得t = $\frac{15}{4}$；乙到达目的地后，300−50 = 60t，得t = $\frac{25}{6}$.故④错误.

3. (2025 西安市期末)一辆大客车和一辆小轿车同时从甲地出发去乙地,匀速而行,大客车到达乙地后停止,小轿车到达乙地后停留4 h,再按照原速从乙地出发返回甲地,小轿车返回甲地后停止.已知两车距甲地的距离s(km)与所用的时间t(h)的关系如图所示.在小轿车从乙地返回甲地的过程中,当两车相遇时,两车出发了______h.

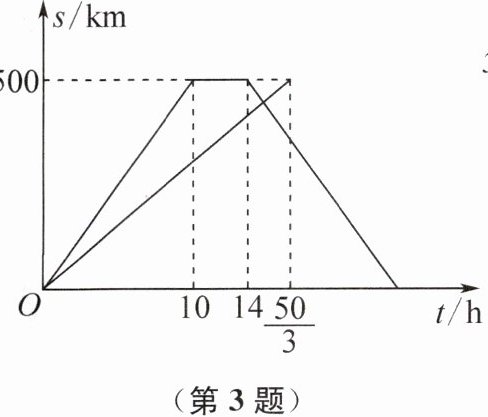
15

答案： 15　提示:大客车距甲地的距离s与所用的时间t的函数表达式为s = 30t(0≤t≤$\frac{50}{3}$).由题意可知，当t = 14时，小轿车正要从乙地返回到达甲地.设小轿车从乙地返回甲地的过程中距甲地的距离s与所用的时间t的函数表达式为s = k₂t + b(k₂,b为常数，且k₂≠0)，把点(14,500)和(24,0)分别代入s = k₂t + b，得$\begin{cases}14k₂ + b = 500\\24k₂ + b = 0\end{cases}$，解得$\begin{cases}k₂ = -50\\b = 1200\end{cases}$，所以小轿车从乙地返回甲地的过程中距甲地的距离s与所用的时间t的函数表达式为s = -50t + 1200(14＜t≤24)，在小轿车从乙地返回甲地的过程中，当两车相遇时，30t = -50t + 1200，解得t = 15，所以小轿车从乙地返回甲地的过程中，当两车相遇时，两车出发了15h.

4. 在A,B两地之间有服务区C,甲车由A地驶往服务区C,乙车由B地驶往A地,两车同时出发,匀速行驶.如图是甲、乙两车分别距离服务区C的路程$y_{甲},y_{乙}(km)$与乙车行驶时间x(h)之间的函数图象,结合图象信息,当两车距服务区C的路程之和是360 km时,乙车的行驶时间为$\frac{18}{13}$h或8h.

答案： $\frac{18}{13}$h或8h　提示:由题意，得$v_{甲}$ = 420÷6 = 70(km/h)，$v_{乙}$ = 120÷2 = 60(km/h)，乙车由B地驶往A地所需的时间为(420 + 120)÷60 = 9(h)，所以点F(9,420).由待定系数法，得$y_{甲}$ = -70x + 420(0≤x≤6)，$y_{乙}$ = $\begin{cases}-60x + 120(0≤x＜2)\\60x - 120(2≤x≤9)\end{cases}$.由题意得，$y_{甲}$ + $y_{乙}$ = 360.分情况讨论:当乙车未到达服务区C，即0≤x＜2时，-70x + 420 + (-60x + 120) = 360，解得x = $\frac{18}{13}$；当乙车经过服务区C，且甲车未到达服务区C，即2≤x＜6时，-70x + 420 + 60x - 120 = 360，解得x = -6(舍去)；当甲车到达服务区C，即6≤x≤9时，$y_{甲}$ = 0，$y_{乙}$ = 360.即60x - 120 = 360，解得x = 8.综上所述，当两车距服务区C的路程之和是360km时，乙车的行驶时间为$\frac{18}{13}$h或8h.

5. (2025 浙江期末)某次假期,小胡和小周去旅行,小胡骑自行车,小周开汽车,两人从甲地出发到乙地,如图表示两人离开甲地的路程y(km)与小胡离开甲地的时间x(h)之间的函数关系.小胡出发2 h后途经一集镇停下休息,然后以原速的$\frac {1}{2}$前行10 km后突然自行车发生故障,小胡立即打电话求助晚出发的小周,此时小周刚好开车行驶到该集镇.小周购买维修自行车的配件所花的时间与再按原速开车到自行车发生故障地所花时间刚好相等.到达故障地后花15 min帮小胡修好自行车.之后小周开车以原速一直前行至乙地,小胡则骑自行车以25 km/h的速度前行至乙地,结果小胡比小周晚到1 h 6 min.
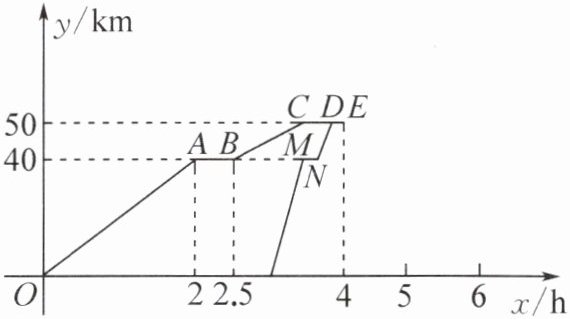
(1)小胡到集镇前的速度是______km/h;小胡休息了______h;小胡休息后至自行车发生故障时的骑车速度是______km/h,这段时间是______h.
(2)小周开车的速度是多少?小胡比小周早出发多少小时?
(3)请你在图中画出修好自行车后小胡、小周行至乙地的过程中y关于x的函数图象.(要求:所画的图象中关键点的坐标必须标出)

答案：
解:
(1)20　0.5　10　1
(2)小胡自行车发生故障，立即打电话求助晚出发的小周，此时小周刚好开车行驶到该集镇，从函数图象可得此时小胡离开甲地的时间为2 + 0.5 + 1 = 3.5(h)，即点C,M的横坐标为3.5，到达故障地后花15min帮小胡修好自行车即函数图象DE段，$\frac{15}{60}$ = 0.25，而点E(4,50)，则点D(3.75,50).因为小周购买维修自行车的配件所花的时间与再按原速开车到自行车发生故障地所花时间刚好相等，所以MN = $\frac{1}{2}$CD = $\frac{1}{2}$×(3.75 - 3.5) = 0.125(h)，所以小周开车的速度是(50 - 40)÷0.125 = 80(km/h)，所以小周从甲地出发到集镇用时为40÷80 = 0.5(h)，则小周出发时，小胡已经出发了3.5 - 0.5 = 3(h)，即小胡比小周早出发3h.
答:小周开车的速度是80km/h，小胡离开甲地的时间比小周早出发3h.
(3)设继续前行S km后到达乙地，则$\frac{S}{80}$+(1 + $\frac{6}{60}$) = $\frac{S}{25}$，解得S = 40，则小胡骑自行车需要的时间为40÷25 = 1.6(h)，小周开车需要的时间为40÷80 = 0.5(h)，修好自行车后小胡、小周行至乙地的过程中y关于x的函数图象如图所示，其中点F(4.5,90)，G(5.6,90).