第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图,∠BAC= 30°,AP平分∠BAC,GF垂直平分线段AP,交AC于点F,Q为射线AB上一动点. 若PQ的最小值为3,则AF的长为(
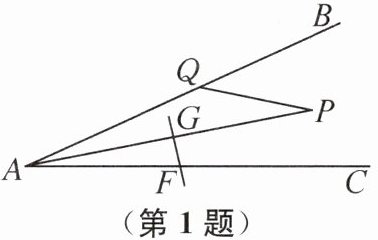
A.3
B.6
C.3√3
D.9
B
)
A.3
B.6
C.3√3
D.9
答案:
B
2. 如图,在△ABC中,AD平分∠BAC,DF⊥AB于点F,E是线段BC的中点,若S△ABC= 6,DF= 2,AC= 7,则AB的长是(
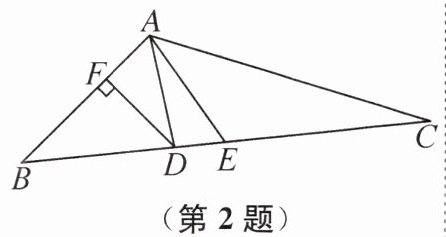
A.3.5
B.4
C.4.5
D.5
D
)
A.3.5
B.4
C.4.5
D.5
答案:
D
3. 如图,∠EOF内有一定点P,过点P的一条直线分别交射线OE于点A,射线OF于点B. 当满足下列哪个条件时,△AOB的面积一定最小( )

A.OA=OB
B.OP为△AOB的角平分线
C.OP为△AOB的高
D.OP为△AOB的中线

A.OA=OB
B.OP为△AOB的角平分线
C.OP为△AOB的高
D.OP为△AOB的中线
答案:
D 提示:当 P 是 AB 的中点,即 PA = PB 时,$S_{\triangle AOB}$最小.理由如下:
如图,过点 P 作一条直线 CD 分别交 OE,OF 于点 C,D,且 PD < PC,过点 A 作 AG//OF 交 CD 于点 G.易证$\triangle APG\cong \triangle BPD$,所以$S_{\triangle APG}=S_{\triangle BPD}$,所以$S_{四边形AODG}=S_{\triangle AOB}$.因为$S_{四边形AODG}<S_{\triangle COD}$,所以$S_{\triangle AOB}<S_{\triangle COD}$(同理,当 PD > PC 时,也可证明$S_{\triangle AOB}<S_{\triangle COD}$),即当 P 是 AB 的中点时,$S_{\triangle AOB}$最小.

D 提示:当 P 是 AB 的中点,即 PA = PB 时,$S_{\triangle AOB}$最小.理由如下:
如图,过点 P 作一条直线 CD 分别交 OE,OF 于点 C,D,且 PD < PC,过点 A 作 AG//OF 交 CD 于点 G.易证$\triangle APG\cong \triangle BPD$,所以$S_{\triangle APG}=S_{\triangle BPD}$,所以$S_{四边形AODG}=S_{\triangle AOB}$.因为$S_{四边形AODG}<S_{\triangle COD}$,所以$S_{\triangle AOB}<S_{\triangle COD}$(同理,当 PD > PC 时,也可证明$S_{\triangle AOB}<S_{\triangle COD}$),即当 P 是 AB 的中点时,$S_{\triangle AOB}$最小.

4.现有下列3个命题:①有两边及其中一边上的高分别对应相等的两个三角形全等;
②有两边及第三边上的高分别对应相等的两个三角形全等;③一边及其他两边上的高分别对应相等的两个三角形全等.其中真命题有
A.0个 B.1个 C.2个 D.3个
答案:
A 提示:判断①的反例:如图1,在$\triangle ABC$和$\triangle AB'C$中,$AC = AC,BC = B'C$,高$AH = AH$,但两个三角形不全等.
判断②的反例:如图2,在$\triangle ABC$和$\triangle ABC'$中,$AB = AB,AC = AC'$,高$AH = AH$,但两个三角形不全等.
判断③的反例:如图3,在$\triangle ABC$中,AD,BE 分别是边 BC,AC 上的高,作$∠BAF = ∠BAC,∠BFA = 90^{\circ }$,延长 BC,FA 交于点$C'$,则在$\triangle ABC$和$\triangle ABC'$中,高$BF = BE,AD = AD,AB = AB$,但$\triangle ABC$与$\triangle ABC'$不全等.



A 提示:判断①的反例:如图1,在$\triangle ABC$和$\triangle AB'C$中,$AC = AC,BC = B'C$,高$AH = AH$,但两个三角形不全等.
判断②的反例:如图2,在$\triangle ABC$和$\triangle ABC'$中,$AB = AB,AC = AC'$,高$AH = AH$,但两个三角形不全等.
判断③的反例:如图3,在$\triangle ABC$中,AD,BE 分别是边 BC,AC 上的高,作$∠BAF = ∠BAC,∠BFA = 90^{\circ }$,延长 BC,FA 交于点$C'$,则在$\triangle ABC$和$\triangle ABC'$中,高$BF = BE,AD = AD,AB = AB$,但$\triangle ABC$与$\triangle ABC'$不全等.



5. 如图,在△ABC中,AB= AC= 12 cm,∠B= ∠C,BC= 8 cm,D为AB的中点. 动点P在线段BC上以2 cm/s的速度由点B点向点C匀速运动,同时,动点Q在线段CA上由点C向点A匀速运动. 若点Q的运动速度为v cm/s,则当△BPD与△CQP全等时,v的值为______
2 或 3
.
答案:
2 或 3 提示:设运动时间为 t s. 因为 AB = $AC = 12cm$,D 为 AB 的中点,所以$BD = \frac{1}{2}AB = 6cm$.由题意,得$BP = 2tcm,CP = (8 - 2t)cm,CQ = vtcm$.因为$∠B = ∠C$,所以①当$\triangle BPD\cong \triangle CQP$时,$BP = CQ,BD = CP$,所以$2t = vt,6 = 8 - 2t$,解得$t = 1,v = 2$;②当$\triangle BPD\cong \triangle CPQ$时,$BP = CP,BD = CQ$,所以$2t = 8 - 2t,6 = vt$,解得$t = 2,v = 3$.综上所述,当 v 的值为 2 或 3 时,$\triangle BPD$与$\triangle CQP$全等.
6. 如图,BD是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点$F,S△ABC= 36 cm^2,AB= 18 cm,BC= 12 cm,$则DE的长为
$\frac{12}{5}$
cm.
答案:
$\frac{12}{5}$ 提示:因为$DE⊥AB$,$DF⊥BC$,所以$DE = DF$.又因为$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle BCD}$,所以$36 = \frac{1}{2}×18DE+\frac{1}{2}×12DF$,所以$DE = \frac{12}{5}cm$.
7. 在△ABC中,高AD,BE所在的直线交于点H,且BH= AC,则∠ABC= ______.
答案:
$45^{\circ }$或$135^{\circ }$ 提示:分三种情况:①如图1,当$\triangle ABC$为锐角三角形,高 AD,BE 均在三角形内部时,易证$\triangle HBD\cong \triangle CAD(AAS)$,所以$BD = AD$,因为$∠ADB = 90^{\circ }$,所以$∠ABC = ∠BAD = 45^{\circ }$;②如图2,当$\triangle ABC$为钝角三角形,且高 AD,BE 分别在三角形外部、内部时,同理易证$\triangle HBD\cong \triangle CAD(AAS)$,所以$AD = BD$,所以$∠DAB = ∠DBA$,因为$∠ADB = 90^{\circ }$,所以$∠ABD = 45^{\circ }$,所以$∠ABC = 180^{\circ } - ∠ABD = 135^{\circ }$;③如图3,当$\triangle ABC$为钝角三角形,且高 AD,BE 均在三角形外部时,同理易证$\triangle HBD\cong \triangle CAD(AAS)$,所以$AD = BD$,所以$∠DAB = ∠DBA$,因为$∠ADB = 90^{\circ }$,所以$∠ABC = ∠ABD = 45^{\circ }$.综上所述,$∠ABC$的度数为$45^{\circ }$或$135^{\circ }$.



$45^{\circ }$或$135^{\circ }$ 提示:分三种情况:①如图1,当$\triangle ABC$为锐角三角形,高 AD,BE 均在三角形内部时,易证$\triangle HBD\cong \triangle CAD(AAS)$,所以$BD = AD$,因为$∠ADB = 90^{\circ }$,所以$∠ABC = ∠BAD = 45^{\circ }$;②如图2,当$\triangle ABC$为钝角三角形,且高 AD,BE 分别在三角形外部、内部时,同理易证$\triangle HBD\cong \triangle CAD(AAS)$,所以$AD = BD$,所以$∠DAB = ∠DBA$,因为$∠ADB = 90^{\circ }$,所以$∠ABD = 45^{\circ }$,所以$∠ABC = 180^{\circ } - ∠ABD = 135^{\circ }$;③如图3,当$\triangle ABC$为钝角三角形,且高 AD,BE 均在三角形外部时,同理易证$\triangle HBD\cong \triangle CAD(AAS)$,所以$AD = BD$,所以$∠DAB = ∠DBA$,因为$∠ADB = 90^{\circ }$,所以$∠ABC = ∠ABD = 45^{\circ }$.综上所述,$∠ABC$的度数为$45^{\circ }$或$135^{\circ }$.



8. 如图,AE是∠CAM的平分线,点B在射线AM上,DE垂直平分BC,交AE于点E,过点E作EF⊥AM于点F. 若∠ACB= 28°,∠EBD= 25°,则∠AED=
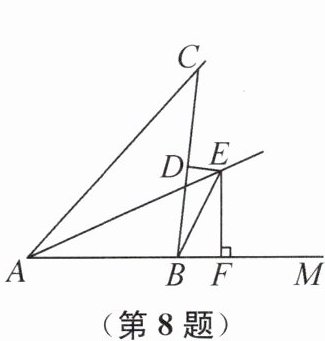

37
°.

答案:
37 提示:连接 CE,过点 E 作$EN⊥AC$于点 N. 因为 DE 垂直平分 BC,所以$∠EDB = 90^{\circ },CE = BE$,所以$∠ECB = ∠EBD = 25^{\circ }$,所以$∠BEC = 180^{\circ } - ∠EBD - ∠ECB = 130^{\circ },∠ACE = ∠ACB + ∠ECB = 53^{\circ }$.因为$EN⊥AC,EF⊥AM$,AE 平分$∠CAM$,所以$EN = EF$.又因为$CE = BE$,所以$Rt\triangle ENC\cong Rt\triangle EFB(HL)$,所以$∠EBF = ∠ACE = 53^{\circ },∠BEF = ∠CEN$.所以$∠BEF + ∠BEN = ∠CEN + ∠BEN$,即$∠NEF = ∠BEC = 130^{\circ }$,所以$∠CAM = 360^{\circ } - ∠ANE - ∠AFE - ∠NEF = 50^{\circ }$,所以$∠BAE = \frac{1}{2}∠CAM = 25^{\circ }$.因为$∠EBF = ∠BAE + ∠AEB = 53^{\circ }$,所以$∠AEB = 28^{\circ }$,所以$∠AED = 90^{\circ } - ∠EBD - ∠AEB = 37^{\circ }$.
9. 如图,在Rt△ABC中,∠ABC= 90°,D是CB延长线上的一点,E是线段AB上一点,连接DE. 已知AC= DE,BC= BE.
(1)求证:AB= DB.
(2)BF平分∠ABC交AC于点F,G是线段FB延长线上的一点,连接DG,H是线段DG上一点,连接AH交BD于点K,连接KG. 当KB平分∠AKG时,求证:AK= DG+KG.
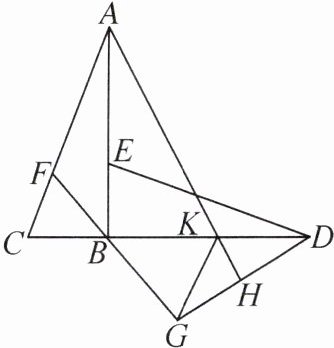
(1)求证:AB= DB.
(2)BF平分∠ABC交AC于点F,G是线段FB延长线上的一点,连接DG,H是线段DG上一点,连接AH交BD于点K,连接KG. 当KB平分∠AKG时,求证:AK= DG+KG.

答案:
证明:
(1) 在$Rt\triangle ACB$和$Rt\triangle DEB$中,$\left\{\begin{array}{l} AC = DE\\ BC = BE\end{array}\right.$,所以$Rt\triangle ACB\cong Rt\triangle DEB$,所以$AB = DB$.
(2) BF平分∠ABC交AC于点F,G是线段FB延长线上的一点,连接DG,H是线段DG上一点,连接AH交BD于点K,连接KG. 当KB平分∠AKG时,求证:AK= DG+KG.证明:作 BM 平分$∠ABD$交 AK 于点 M.因为 BF 平分$∠ABC$,BM 平分$∠ABD$,KB 平分$∠AKG,∠ABC = ∠ABD = 90^{\circ }$,所以$∠CBF = ∠ABF = 45^{\circ },∠ABM = ∠MBK = 45^{\circ },∠MKB = ∠GKB$.因为$∠GBK = ∠CBF = 45^{\circ }$,所以$∠MBK = ∠GBK$.在$\triangle BMK$和$\triangle BGK$中,$\left\{\begin{array}{l} ∠MBK = ∠GBK\\ BK = BK\\ ∠MKB = ∠GKB\end{array}\right.$,所以$\triangle BMK\cong \triangle BGK$,所以$BM = BG,KM = KG$.
在$\triangle ABM$和$\triangle DBG$中,$\left\{\begin{array}{l} AB = DB\\ ∠ABM = ∠DBG\\ BM = BG\end{array}\right.$,所以$\triangle ABM\cong \triangle DBG$,所以$AM = DG$.因为$AK = AM + KM$,所以$AK = DG + KG$.
(1) 在$Rt\triangle ACB$和$Rt\triangle DEB$中,$\left\{\begin{array}{l} AC = DE\\ BC = BE\end{array}\right.$,所以$Rt\triangle ACB\cong Rt\triangle DEB$,所以$AB = DB$.
(2) BF平分∠ABC交AC于点F,G是线段FB延长线上的一点,连接DG,H是线段DG上一点,连接AH交BD于点K,连接KG. 当KB平分∠AKG时,求证:AK= DG+KG.证明:作 BM 平分$∠ABD$交 AK 于点 M.因为 BF 平分$∠ABC$,BM 平分$∠ABD$,KB 平分$∠AKG,∠ABC = ∠ABD = 90^{\circ }$,所以$∠CBF = ∠ABF = 45^{\circ },∠ABM = ∠MBK = 45^{\circ },∠MKB = ∠GKB$.因为$∠GBK = ∠CBF = 45^{\circ }$,所以$∠MBK = ∠GBK$.在$\triangle BMK$和$\triangle BGK$中,$\left\{\begin{array}{l} ∠MBK = ∠GBK\\ BK = BK\\ ∠MKB = ∠GKB\end{array}\right.$,所以$\triangle BMK\cong \triangle BGK$,所以$BM = BG,KM = KG$.
在$\triangle ABM$和$\triangle DBG$中,$\left\{\begin{array}{l} AB = DB\\ ∠ABM = ∠DBG\\ BM = BG\end{array}\right.$,所以$\triangle ABM\cong \triangle DBG$,所以$AM = DG$.因为$AK = AM + KM$,所以$AK = DG + KG$.
查看更多完整答案,请扫码查看


