第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
7. 凸四边形是指四边形内任意两点间的线段全部位于该四边形内部,且四个内角均小于180°的四边形.在平面直角坐标系中,已知凸四边形AOBC的边OA= OB= BC≠AC,且点O(0,0),点A(0,16),点B在x轴的正半轴.如果对角线OC把四边形AOBC分割成了两个等腰三角形,那么点C的坐标为______.
答案:
(8,8√3)或(16+8√3,8) 提示:因为OB=BC=16,所以△OBC是等腰三角形,所以当对角线OC把四边形AOBC分割成了两个等腰三角形时,△OAC也是等腰三角形,因为OA≠AC,所以有以下两种情况:①当OC=OA=16时,过点C作CD⊥x轴于点D,如图1所示.因为OC=OA=OB=BC=16,所以△OBC是等边三角形,所以OD=BD=1/2OB=8.在Rt△OCD中,由勾股定理,得CD=√(OC² - OD²)=8√3,所以点C的坐标为(8,8√3).

②当AC=OC时,过点C分别作CE⊥y轴于点E,CF⊥x轴于点F,如图2所示.易得AE=OE=8,CF=OE=8,OF=OB+BF=16+BF.在Rt△BCF中,BC=16,CF=8,由勾股定理,得BF=√(BC² - CF²)=8√3,所以OF=16+8√3,所以点C的坐标为(16+8√3,8).综上所述,点C的坐标为(8,8√3)或(16+8√3,8).

(8,8√3)或(16+8√3,8) 提示:因为OB=BC=16,所以△OBC是等腰三角形,所以当对角线OC把四边形AOBC分割成了两个等腰三角形时,△OAC也是等腰三角形,因为OA≠AC,所以有以下两种情况:①当OC=OA=16时,过点C作CD⊥x轴于点D,如图1所示.因为OC=OA=OB=BC=16,所以△OBC是等边三角形,所以OD=BD=1/2OB=8.在Rt△OCD中,由勾股定理,得CD=√(OC² - OD²)=8√3,所以点C的坐标为(8,8√3).

②当AC=OC时,过点C分别作CE⊥y轴于点E,CF⊥x轴于点F,如图2所示.易得AE=OE=8,CF=OE=8,OF=OB+BF=16+BF.在Rt△BCF中,BC=16,CF=8,由勾股定理,得BF=√(BC² - CF²)=8√3,所以OF=16+8√3,所以点C的坐标为(16+8√3,8).综上所述,点C的坐标为(8,8√3)或(16+8√3,8).

8. 如图,已知A为y轴正半轴上一点,B为x轴正半轴上一点,以AB为斜边作等腰直角三角形ABC,A,B,C按顺时针方向排列.若AB= 10,△AOB的面积为24,则点C的坐标为______.


答案:
(-1,1)或(1,-1) 提示:设点A(0,a),B(b,0),且由题意知,a>0,b>0,则有{a²+b²=100,1/2ab=24.所以{(a+b)²=196,(a - b)²=4,所以{a+b=14,a - b=2或{a+b=14,a - b=-2,解得{a=8,b=6或{a=6,b=8.如图,过点C作CH⊥y轴于点H,过点B作BG⊥CH,交CH所在直线于点G.易证△AHC≌△CGB.所以AH=CG,CH=BG.设点C(m,n).如图1,当{a=8,b=6时,AH=8 - n,CH=-m,CG=6 - m,BG=n,所以{8 - n=6 - m,-m=n,解得{m=-1,n=1,所以点C(-1,1);如图2,当{a=6,b=8时,AH=6 - n,CH=m,CG=8 - m,BG=-n,所以{6 - n=8 - m,m=-n,解得{m=1,n=-1,所以点C(1,-1).综上所述,点C的坐标为(-1,1)或(1,-1).


(-1,1)或(1,-1) 提示:设点A(0,a),B(b,0),且由题意知,a>0,b>0,则有{a²+b²=100,1/2ab=24.所以{(a+b)²=196,(a - b)²=4,所以{a+b=14,a - b=2或{a+b=14,a - b=-2,解得{a=8,b=6或{a=6,b=8.如图,过点C作CH⊥y轴于点H,过点B作BG⊥CH,交CH所在直线于点G.易证△AHC≌△CGB.所以AH=CG,CH=BG.设点C(m,n).如图1,当{a=8,b=6时,AH=8 - n,CH=-m,CG=6 - m,BG=n,所以{8 - n=6 - m,-m=n,解得{m=-1,n=1,所以点C(-1,1);如图2,当{a=6,b=8时,AH=6 - n,CH=m,CG=8 - m,BG=-n,所以{6 - n=8 - m,m=-n,解得{m=1,n=-1,所以点C(1,-1).综上所述,点C的坐标为(-1,1)或(1,-1).


9. 【类比学习】一动点沿着数轴向右平移3个单位长度,再向左平移2个单位长度,相当于向右平移1个单位长度.用实数加法表示为3+(-2)= 1.若坐标平面上的点作如下平移:沿x轴方向平移a(向右为正,向左为负,平移|a|个单位长度),沿y轴方向平移b(向上为正,向下为负,平移|b|个单位长度),则把有序数对{a,b}叫作这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}= {a+c,b+d}.
【解决问题】
(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到点A,再按照“平移量”{1,2}平移到点B.若先把动点P按照“平移量”{1,2}平移到点C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?如果是,请在图1中画出四边形OABC;如果不是,请说明理由.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.

【解决问题】
(1)计算:{3,1}+{1,2};{1,2}+{3,1}.
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到点A,再按照“平移量”{1,2}平移到点B.若先把动点P按照“平移量”{1,2}平移到点C,再按照“平移量”{3,1}平移,最后的位置还是点B吗?如果是,请在图1中画出四边形OABC;如果不是,请说明理由.
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.

答案:
解:
(1){3,1}+{1,2}={4,3};{1,2}+{3,1}={4,3}.
(2)最后的位置仍是点B,画图如图所示.
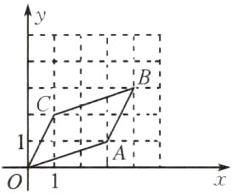
(3){2,3}+{3,2}+{-5,-5}={0,0}.
解:
(1){3,1}+{1,2}={4,3};{1,2}+{3,1}={4,3}.
(2)最后的位置仍是点B,画图如图所示.

(3){2,3}+{3,2}+{-5,-5}={0,0}.
10. 如图1,在平面直角坐标系中,点A(a,0),B(0,b),C(1,-3),其中a,b满足关系式$\sqrt{a-3}+(a+b-7)^2= 0$.平移AC使点A与点B重合,点C的对应点为点D.
(1)直接写出A,D两点的坐标,则A(______,______),D(______,______).
(2)如图1,过点D作DE⊥y轴于点E,猜想∠CAG与∠BDE数量关系,并说明理由.
(3)如图2,过点C作CF//x轴交y轴于点F,Q为x轴上点A左侧的一动点,连接QC,CM平分∠QCA,CN平分∠FCA,则当点Q运动时,$\frac{∠MCN}{∠AQC}$的值是否变化?如果变化,请说明理由;如果不变,请求出其值.

(1)直接写出A,D两点的坐标,则A(______,______),D(______,______).
(2)如图1,过点D作DE⊥y轴于点E,猜想∠CAG与∠BDE数量关系,并说明理由.
(3)如图2,过点C作CF//x轴交y轴于点F,Q为x轴上点A左侧的一动点,连接QC,CM平分∠QCA,CN平分∠FCA,则当点Q运动时,$\frac{∠MCN}{∠AQC}$的值是否变化?如果变化,请说明理由;如果不变,请求出其值.

答案:
解:
(1)3 0 -2 1
(2)∠BDE+∠CAG=180°.理由如下:如图,延长DE交CA的延长线于点T.因为DE⊥y轴,所以DT//OG,所以∠T+∠OAT=180°.因为BD//CT,所以∠BDE=∠T.因为∠CAG=∠OAT,所以∠BDE+∠CAG=180°.

(3)不变,∠MCN/∠AQC=1/2.理由如下:设∠AQC=y,∠MCN=x,∠ACM=z.因为CF//AQ,所以∠FCQ=∠AQC=y.因为∠ACM=∠QCM=z,所以∠QCN=z - x.因为∠FCN=∠ACN,所以y+(z - x)=x+z,所以y=2x,即∠AQC=2∠MCN,所以∠MCN/∠AQC=1/2.
解:
(1)3 0 -2 1
(2)∠BDE+∠CAG=180°.理由如下:如图,延长DE交CA的延长线于点T.因为DE⊥y轴,所以DT//OG,所以∠T+∠OAT=180°.因为BD//CT,所以∠BDE=∠T.因为∠CAG=∠OAT,所以∠BDE+∠CAG=180°.

(3)不变,∠MCN/∠AQC=1/2.理由如下:设∠AQC=y,∠MCN=x,∠ACM=z.因为CF//AQ,所以∠FCQ=∠AQC=y.因为∠ACM=∠QCM=z,所以∠QCN=z - x.因为∠FCN=∠ACN,所以y+(z - x)=x+z,所以y=2x,即∠AQC=2∠MCN,所以∠MCN/∠AQC=1/2.
查看更多完整答案,请扫码查看


