第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形和中间的小正方形 MNPQ 拼成的一个大正方形 ABCD. 连接 AQ,BP,CN,DM. 若正方形 ABCD 的面积为 2a,阴影部分的面积为 2b. 则 AN 的长度为 (

A.a+b
$B.a^2+b^2$
C.√(a+b)
$D.√(a^2+b^2)$
C
)
A.a+b
$B.a^2+b^2$
C.√(a+b)
$D.√(a^2+b^2)$
答案:
C 提示:设MN=x,AM=y,则DN=AM=y,AN=AM+MN=y+x.在Rt△AND中,2a=S正方形ABCD=AD²=AN²+DN²=(y+x)²+y²①.由S阴影=4S△MND+S正方形MNPQ,得2b=4×$\frac{1}{2}$xy+x²=2xy+x²=(y+x)²-y²②.(①+②)÷2,得a+b=(y+x)².所以AN=y+x=$\sqrt{a+b}$(负值已舍).
2. 如图,在△ABC 中,AB= AC,直线 m,n 分别是 AB,AC 的垂直平分线,m,n 交于点 P,连接 CP. 若∠1= 21°,则∠B 的度数为 ______.


答案:
67° 提示:如图,连接PA,PB,设直线m交AC于点D,设∠PAC=α.因为直线m,n分别是AB,AC的垂直平分线,m,n交于点P,所以PA=PB,PA=PC,所以PB=PA=PC,∠PCA=∠PAC=α.又因为AB=AC,所以点P,A都在线段BC的垂直平分线上,即PA垂直平分BC.所以∠PAB=∠PAC=α,所以∠BAC=∠PAB+∠PAC=2α.因为∠1=21°,所以∠PDA=∠1+∠PCA=21°+α.易知∠PDA+∠BAC=90°,所以21°+α+2α=90°,解得α=23°,所以∠BAC=2α=46°,所以∠ABC=∠ACB=$\frac{1}{2}$(180°-∠BAC)=67°.

67° 提示:如图,连接PA,PB,设直线m交AC于点D,设∠PAC=α.因为直线m,n分别是AB,AC的垂直平分线,m,n交于点P,所以PA=PB,PA=PC,所以PB=PA=PC,∠PCA=∠PAC=α.又因为AB=AC,所以点P,A都在线段BC的垂直平分线上,即PA垂直平分BC.所以∠PAB=∠PAC=α,所以∠BAC=∠PAB+∠PAC=2α.因为∠1=21°,所以∠PDA=∠1+∠PCA=21°+α.易知∠PDA+∠BAC=90°,所以21°+α+2α=90°,解得α=23°,所以∠BAC=2α=46°,所以∠ABC=∠ACB=$\frac{1}{2}$(180°-∠BAC)=67°.

3. 在长方形 ABCD 中,AD= 6,E,F 分别是边 AD,AB 上的动点. 在长方形 ABCD 的内部(包含边界),以 EF 为直角边作等腰直角三角形 EFP,且∠EFP= 90°. 过点 P 作 PQ⊥AB,垂足为 Q.

(1)如图 1,当 AE= 1 时,设 AQ= x,PQ= y,求 y 与 x 之间的函数表达式.
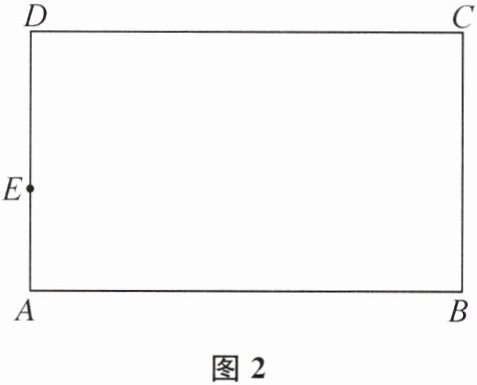
(2)当点 E 的位置如图 2 所示时,点 F 在边 AB 上运动,用直尺和圆规在图 2 中作出所有满足条件的点 P(保留作图痕迹,写出必要的文字说明).
(3)当点 E,F 分别在边 AD,AB 上运动时,满足条件的点 P 所形成区域的面积随着 AB 的长度变化而变化,设点 P 所形成区域的面积为 S,AB 的长度为 n. 请直接写出 S 与 n 的函数表达式及对应 n 的取值范围.

(1)如图 1,当 AE= 1 时,设 AQ= x,PQ= y,求 y 与 x 之间的函数表达式.
(2)当点 E 的位置如图 2 所示时,点 F 在边 AB 上运动,用直尺和圆规在图 2 中作出所有满足条件的点 P(保留作图痕迹,写出必要的文字说明).
(3)当点 E,F 分别在边 AD,AB 上运动时,满足条件的点 P 所形成区域的面积随着 AB 的长度变化而变化,设点 P 所形成区域的面积为 S,AB 的长度为 n. 请直接写出 S 与 n 的函数表达式及对应 n 的取值范围.

答案:
3. 解:
(1)因为△EFP是等腰直角三角形,且∠EFP=90°,所以EF=FP.因为四边形ABCD是长方形,PQ⊥AB,所以∠A=∠PQF=90°,所以∠AFE=90°-∠PFQ=∠QPF.可证△AEF≌△QFP(AAS),所以FA=PQ=y,AE=QF=1.因为AQ=FA+QF,所以x=y+1,即y=x-1.
(2)原理:由
(1)可知,点P在以A为原点,AB,AD所在直线为x轴、y轴的平面直角坐标系中的函数y=x - AE的图象上运动,再根据两点确定一条直线即可作出满足条件的点P.
作法:如图1,在边AB上取点N,使得AN=AE,在边AB上任取一点F,连接EF,过点F作PF⊥EF,PF=EF,连接NP并延长,交DC于点M,则线段MN即为所有满足条件的点P的轨迹.

(3)$S=\begin{cases} \frac{1}{2}n^{2}(0 < n \leq 6), \\ -\frac{1}{2}n^{2}+12n-36(6 < n < 12), \\ 36(n \geq 12). \end{cases}$
提示:①当0<n≤6时,如图2,当点E与点A重合,点F在边AB上运动时,点P的轨迹为线段AG,且∠BAG=45°,当点F与点A重合,点E在边AD上运动时,点P的轨迹为线段AB,当点E,F均运动时,点P所形成的区域为等腰直角三角形ABG,所以S=$\frac{1}{2}n^{2}$;②当6<n<12时,如图3,同理可得,点P所形成的区域为多边形ANPCM,由
(1)可得PB=FA=AB - FB=AB - AD=n - 6,同理可得,△ADM,△PBN均是等腰直角三角形,所以S=6n - $\frac{1}{2}×6^{2}-\frac{1}{2}(n - 6)^{2}=-\frac{1}{2}n^{2}+12n - 36$;③当n = 12时,如图4,PB=AD=6,AF=FB=6,所以S=6×12 - 6×6=36;④当n>12时,如图5,易知四边形AFPM为平行四边形,所以S=S四边形AFPM=6×6=36.综上所述,S=$\begin{cases} \frac{1}{2}n^{2}(0 < n \leq 6), \\ -\frac{1}{2}n^{2}+12n - 36(6 < n < 12), \\ 36(n \geq 12). \end{cases}$




3. 解:
(1)因为△EFP是等腰直角三角形,且∠EFP=90°,所以EF=FP.因为四边形ABCD是长方形,PQ⊥AB,所以∠A=∠PQF=90°,所以∠AFE=90°-∠PFQ=∠QPF.可证△AEF≌△QFP(AAS),所以FA=PQ=y,AE=QF=1.因为AQ=FA+QF,所以x=y+1,即y=x-1.
(2)原理:由
(1)可知,点P在以A为原点,AB,AD所在直线为x轴、y轴的平面直角坐标系中的函数y=x - AE的图象上运动,再根据两点确定一条直线即可作出满足条件的点P.
作法:如图1,在边AB上取点N,使得AN=AE,在边AB上任取一点F,连接EF,过点F作PF⊥EF,PF=EF,连接NP并延长,交DC于点M,则线段MN即为所有满足条件的点P的轨迹.

(3)$S=\begin{cases} \frac{1}{2}n^{2}(0 < n \leq 6), \\ -\frac{1}{2}n^{2}+12n-36(6 < n < 12), \\ 36(n \geq 12). \end{cases}$
提示:①当0<n≤6时,如图2,当点E与点A重合,点F在边AB上运动时,点P的轨迹为线段AG,且∠BAG=45°,当点F与点A重合,点E在边AD上运动时,点P的轨迹为线段AB,当点E,F均运动时,点P所形成的区域为等腰直角三角形ABG,所以S=$\frac{1}{2}n^{2}$;②当6<n<12时,如图3,同理可得,点P所形成的区域为多边形ANPCM,由
(1)可得PB=FA=AB - FB=AB - AD=n - 6,同理可得,△ADM,△PBN均是等腰直角三角形,所以S=6n - $\frac{1}{2}×6^{2}-\frac{1}{2}(n - 6)^{2}=-\frac{1}{2}n^{2}+12n - 36$;③当n = 12时,如图4,PB=AD=6,AF=FB=6,所以S=6×12 - 6×6=36;④当n>12时,如图5,易知四边形AFPM为平行四边形,所以S=S四边形AFPM=6×6=36.综上所述,S=$\begin{cases} \frac{1}{2}n^{2}(0 < n \leq 6), \\ -\frac{1}{2}n^{2}+12n - 36(6 < n < 12), \\ 36(n \geq 12). \end{cases}$




查看更多完整答案,请扫码查看


