第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 比较$2,\sqrt{5},\sqrt[3]{7}$的大小,正确的是 (
A.$2<\sqrt{5}<\sqrt[3]{7}$
B.$2<\sqrt[3]{7}<\sqrt{5}$
C.$\sqrt[3]{7}<2<\sqrt{5}$
D.$\sqrt{5}<\sqrt[3]{7}<2$
C
)A.$2<\sqrt{5}<\sqrt[3]{7}$
B.$2<\sqrt[3]{7}<\sqrt{5}$
C.$\sqrt[3]{7}<2<\sqrt{5}$
D.$\sqrt{5}<\sqrt[3]{7}<2$
答案:
C
2. 已知点$M(a,b),N(c,d)$是一次函数$y= 2x+1$图象上的两个点,若点$P(3a,3b)$在如图所示的位置,则下列可能表示$(3c,3d)$的点是 (
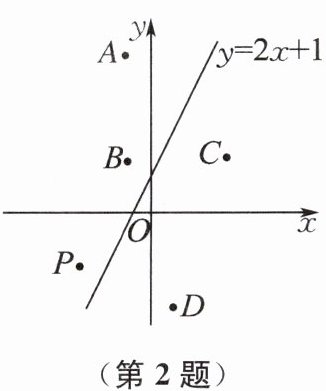
A.A
B.B
C.C
D.D
B
)
A.A
B.B
C.C
D.D
答案:
B 提示:因为点M(a,b)在直线y=2x+1上,所以b=2a+1.所以点P(3a,6a+3),所以点P在直线y=2x+3上.同理,点(3c,3d)也在直线y=2x+3上.易知直线y=2x+3与直线y=2x+1平行.连接PA,PB,PC,PD.由题图可知,只有直线PB与直线y=2x+1平行,所以表示(3c,3d)的点是B.
3. 已知直线$y= kx+3与直线y= ax+6的交点横坐标是-3$,现有下列结论:①$k>0$;②$|k|<|a|$;③方程$kx+3= ax+6的解是x= -3$;④不等式$kx+3>ax+6的解集是x<-3$.其中所有正确结论的序号是 ( )
A.①②
B.②③
C.③④
D.③
A.①②
B.②③
C.③④
D.③
答案:
C 提示:根据题意画出几种可能的图象,如图所示.由图象可知,①②错误,③④正确.



C 提示:根据题意画出几种可能的图象,如图所示.由图象可知,①②错误,③④正确.



4. 如图,一次函数$y= x+4的图象与x$轴、$y轴分别交于点A,B$,$C是线段AO$上一定点,$E,F分别为直线y= x+4和y$轴上的两个动点,当$\triangle CEF$周长的最小值为6时,点$C$的坐标为 (
A.$(-1,0)$
B.$(-\sqrt{2},0)$
C.$(-\sqrt{3},0)$
D.$(-2,0)$
B
)A.$(-1,0)$
B.$(-\sqrt{2},0)$
C.$(-\sqrt{3},0)$
D.$(-2,0)$
答案:
B 提示:分别作点C关于y轴和直线y=x+4的对称点G,D,连接AD,DG,交AB于点E,交y轴于点F,所以DE=CE,GF=CF,所以CE+CF+EF=DE+GF+EF≥DG,当点D,E,F,G在同一直线上时,△CEF的周长最小,为DG=6.易求点A(-4,0),B(0,4),所以OA=OB,△AOB是等腰直角三角形.因为点C,D关于AB对称,所以∠DAB=∠BAC=45°,所以∠DAC=90°.设点C(-c,0),则AD=AC=-c+4,OG=OC=c,所以AG=AO+OG=4+c.在Rt△ADG中,由勾股定理,得DG²=AD²+AG²,即6²=(4-c)²+(4+c)²,解得c=√2(负值已舍),即点C(-√2,0).
5. 定义:在平面直角坐标系中,若点$A到x$轴、$y$轴的距离之和为2,则称点$A$为“成双点”.例如:如图,点$B(-1.5,0.5)到x$轴、$y轴的距离分别为0.5,1.5$,距离之和为2,则点$B$是“成双点”;点$C(1,1)$,$D(-0.8,-1.2)$也是“成双点”.一次函数$y= kx+b(k≠0)的图象l经过点(-3,-4)$,且图象$l$上存在“成双点”,则$k$的取值范围为 ( )
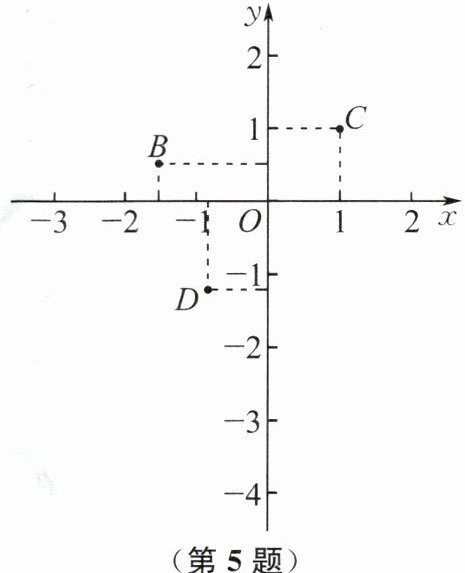
A.$\frac{2}{3}\leqslant k\leqslant 2$
B.$\frac{4}{5}\leqslant k\leqslant 2$
C.$\frac{4}{5}\leqslant k\leqslant 4$
D.$\frac{2}{3}\leqslant k\leqslant 4$
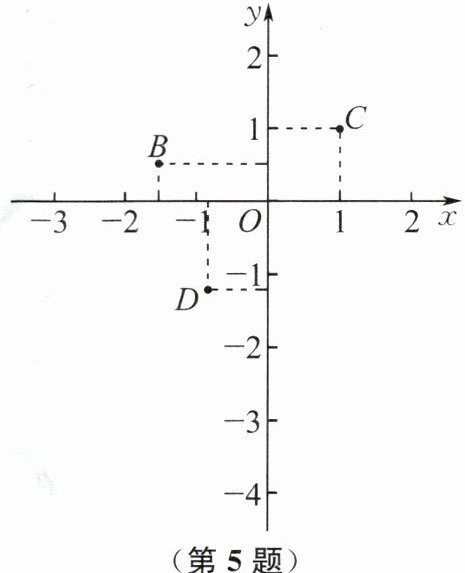
A.$\frac{2}{3}\leqslant k\leqslant 2$
B.$\frac{4}{5}\leqslant k\leqslant 2$
C.$\frac{4}{5}\leqslant k\leqslant 4$
D.$\frac{2}{3}\leqslant k\leqslant 4$
答案:
D 提示:如图,取点E(-2,0),F(2,0),G(0,-2),H(0,2),连接EG,FG,EH,FH.在线段EG上取点P,过点P分别作PM⊥x轴,PN⊥y轴,垂足分别为M,N,则PN=OM.因为OE=OF=OG=2,所以△OEG,△OFG均为等腰直角三角形,所以∠OEG=45°,所以△PEM为等腰直角三角形,所以PM=EM,所以PM+PN=OE=2,所以P是“成双点”,即线段EG上的点均为“成双点”.同理,线段FG,EH,FH上的点也均为“成双点”.因为一次函数的图象l经过点(-3,-4),所以观察图象可知,当一次函数y=kx+b(k≠0)的图象l与线段EG有交点时,一次函数y=kx+b(k≠0)的图象l上存在“成双点”.又因为-3k+b=-4,解得b=3k-4,所以一次函数的表达式为y=kx+3k-4.当一次函数y=kx+b(k≠0)的图象l经过点E时,-2k+3k-4=0,解得k=4;当一次函数y=kx+b(k≠0)的图象l经过点G时,3k-4=-2,解得k=2/3.所以k的取值范围为2/3≤k≤4.

D 提示:如图,取点E(-2,0),F(2,0),G(0,-2),H(0,2),连接EG,FG,EH,FH.在线段EG上取点P,过点P分别作PM⊥x轴,PN⊥y轴,垂足分别为M,N,则PN=OM.因为OE=OF=OG=2,所以△OEG,△OFG均为等腰直角三角形,所以∠OEG=45°,所以△PEM为等腰直角三角形,所以PM=EM,所以PM+PN=OE=2,所以P是“成双点”,即线段EG上的点均为“成双点”.同理,线段FG,EH,FH上的点也均为“成双点”.因为一次函数的图象l经过点(-3,-4),所以观察图象可知,当一次函数y=kx+b(k≠0)的图象l与线段EG有交点时,一次函数y=kx+b(k≠0)的图象l上存在“成双点”.又因为-3k+b=-4,解得b=3k-4,所以一次函数的表达式为y=kx+3k-4.当一次函数y=kx+b(k≠0)的图象l经过点E时,-2k+3k-4=0,解得k=4;当一次函数y=kx+b(k≠0)的图象l经过点G时,3k-4=-2,解得k=2/3.所以k的取值范围为2/3≤k≤4.

6. 如图,在等腰直角三角形$ABC$中,$\angle A= 90^{\circ}$,$BD平分\angle ABC$,$BE平分\angle DBC$,$M,N分别为射线BE,BC$上的动点.若$BD= 8$,则$CM+MN$的最小值为(
A.4
B.6
C.8
D.10
A
)A.4
B.6
C.8
D.10
答案:
A 提示:作点N关于BE的对称点N',则MN=MN',过点C作CF⊥BD,交BD的延长线于点F,过点D作DG⊥BC于点G.因为CM+MN=CM+MN'≥CN'≥CF,所以当C,M,N'三点共线,且CN'⊥BD时,CM+MN的值最小,最小值为CF的长.因为BD平分∠ABC,AD⊥AB,DG⊥BC,所以AD=DG.易证△CDG是等腰直角三角形,所以CD=√2DG=√2AD.设AD=a,则AB=AC=AD+CD=(1+√2)a,BC=√2AC=(√2+2)a.在Rt△ABD中,由勾股定理,得BD²=AD²+AB²,即8²=a²+[(1+√2)a]²,解得a²=32-16√2.因为S△BDC=1/2BC·DG=1/2BD·CF,所以CF=(BC·DG)/BD=((√2+2)a·a)/8=((√2+2)(32-16√2))/8=(32√2-32+64-32√2)/8=4.
7. 已知在$\triangle ABC$中,$AB= AC= 8$,$\angle BAC= 30^{\circ}$.将$\triangle ABC绕点A$逆时针旋转,使点$B落在原\triangle ABC的点C$处,此时点$C落在点D$处.延长线段$AD$,交原$\triangle ABC的边BC的延长线于点E$,那么线段$DE$的长等于______.
答案:
4√3-4 提示:如图,过点C作CH⊥AD,垂足为H.因为△ABC绕点A逆时针旋转得到△ACD,所以AB=AC=AD=8,∠BAC=∠CAD=30°,CH=1/2AC=4.所以AH=√(AC²-CH²)=4√3,∠B=∠ACB=∠ACD=∠ADC=75°.所以∠E=∠ACB-∠CAD=45°,所以HE=CH=4,所以AE=4√3+4.因为AD=8,所以DE=AE-AD=4√3+4-8=4√3-4.

4√3-4 提示:如图,过点C作CH⊥AD,垂足为H.因为△ABC绕点A逆时针旋转得到△ACD,所以AB=AC=AD=8,∠BAC=∠CAD=30°,CH=1/2AC=4.所以AH=√(AC²-CH²)=4√3,∠B=∠ACB=∠ACD=∠ADC=75°.所以∠E=∠ACB-∠CAD=45°,所以HE=CH=4,所以AE=4√3+4.因为AD=8,所以DE=AE-AD=4√3+4-8=4√3-4.

8. 观察以下几组勾股数:①3,4,5;②5,12,13;③7,24,25;④9,40,41.请寻找规律,写出第$n$组勾股数:
2n+1,2n²+2n,2n²+2n+1
.
答案:
2n+1,2n²+2n,2n²+2n+1
查看更多完整答案,请扫码查看


