《2025年小题狂做八年级数学上册苏科版巅峰版》

1. 已知x,y满足$\sqrt{3x+4}+y^{2}-6y+9= 0$,则xy的值是(B)
A.4
B.-4
C.$\frac{9}{4}$
D.$-\frac{9}{4}$

答案： B

2. 甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20 km,他们前进的路程为s(km),甲前进的时间为t(h),甲、乙前进的路程与时间之间的函数图象如图所示,则乙追上甲时乙所用的时间为(C)
A.1 h
B.1.2 h
C.$\frac{1}{3}$ h
D.1.5 h

答案： C

3. 如图,在$\triangle ABC$中,$\angle ABC= 90^{\circ}$,$AB= 3$,$BC= 8$,D为边AC上的一个动点,连接BD,E为BD上的一个动点,连接AE,CE.当$\angle ABD= \angle BCE$时,线段AE长的最小值是(D)

A.2.5
B.2
C.1.5
D.1

答案： D 提示:取 BC 的中点 T,连接 AT,ET.因为∠ABC=90°,所以∠ABD+∠CBD=90°.因为∠ABD=∠BCE,所以∠CBD+∠BCE=90°,所以∠CEB=90°.因为 CT=BT,所以 ET=BT=$\frac{1}{2}$BC=4.由勾股定理,得 AT=$\sqrt{AB^2+BT^2}$=5.因为 AE≥AT - ET,即 AE≥1,当 A,E,T 三点共线时等号成立.所以 AE 长的最小值为 1.

4. 如图,在长方形ABCD中,$AB= 18$,$AD= 8$,E为边CD上的一点,$CE= 12$,点P从点B出发,以每秒2个单位长度的速度沿着边BA向终点A运动,连接PE.设点P运动的时间为t s,则当$\triangle PAE$为等腰三角形时,t的值为(D)
A.3
B.$\frac{22}{5}$
C.$\frac{7}{2}或\frac{29}{6}$
D.3或4或$\frac{29}{6}$

答案： D 提示:因为四边形 ABCD 是长方形,所以∠D=90°,CD=AB=18.因为 CE=12,所以 DE=6.在 Rt△ADE 中,根据勾股定理,得 AE=$\sqrt{8^2+6^2}$=10.过点 E 作 EM⊥AB 于点 M,则 AM=DE=6.若△PAE 是等腰三角形,则有三种可能:当 EP=EA 时,AP=2AM=12,所以 t=$\frac{BP}{2}$=$\frac{18 - 12}{2}$=3;当 AP=EA=10 时,BP=18 - 10=8,所以 t=$\frac{8}{2}$=4;当 EP=AP 时,在 Rt△EPM 中,由勾股定理,可得(12 - 2t)^2+8^2=(18 - 2t)^2,解得 t=$\frac{29}{6}$.综上所述,符合要求的 t 的值为 3 或 4 或$\frac{29}{6}$.

5. 如图,已知在平面直角坐标系中,x轴上的动点P(x,0)到定点A(0,2),B(3,1)的距离分别为PA和PB,则PA+PB的最小值为$3\sqrt{2}$.

答案： $3\sqrt{2}$ 提示:作点 B 关于 x 轴的对称点 B',连接 PB',则 PB'=PB,点 B'(3, - 1),所以 PA+PB=PA+PB'.当 A,P,B'三点在同一条直线上时,PA + PB 的值最小,最小值为 AB'的长.因为 AB'=$\sqrt{3^2+3^2}$=$3\sqrt{2}$,所以 PA+PB 的最小值为$3\sqrt{2}$.

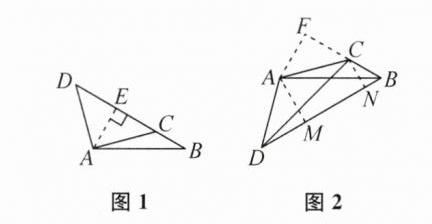
6. 已知$\triangle ABC与\triangle ABD$在同一平面内,点C,D不关于AB对称,$\angle ABC= \angle ABD= 30^{\circ}$,$AB= 2$,$AC= AD= \sqrt{2}$,则CD的长为______.

答案：
2 或$\sqrt{6}$ 提示:分两种情况:①如图 1,当点 C,D 在直线 AB 同侧时,过点 A 作 AE⊥BD 于点 E.因为∠ABC=30°,∠AEB=90°,所以 AE=$\frac{1}{2}$AB=1.由勾股定理,得 CE=$\sqrt{AC^2 - AE^2}$=1.因为 DE=CE=1,所以 CD=CE+DE=2.②如图 2,当点 C,D 在直线 AB 异侧时,过点 A 分别作 AM⊥BD 于点 M,AF⊥BC 交 BC 延长线于点 F,过点 C 作 CN⊥BD 于点 N.同
(1),得 AF=AM=$\frac{1}{2}$AB=1,由勾股定理,得 BM=BF=$\sqrt{AB^2 - AF^2}$=$\sqrt{3}$,DM=CF=$\sqrt{AC^2 - AF^2}$=1,所以 BD=DM+BM=1+$\sqrt{3}$,BC=BF - CF=$\sqrt{3}$ - 1.在 Rt△BCN 中,∠CBN=∠ABC+∠ABD=60°,∠BCN=90° - ∠CBN=30°,所以 BN=$\frac{1}{2}$BC=$\frac{\sqrt{3}-1}{2}$,CN=$\frac{\sqrt{3}}{2}$BC=$\frac{\sqrt{3}(\sqrt{3}-1)}{2}$=$\frac{3-\sqrt{3}}{2}$,所以 DN=BD - BN=1+$\sqrt{3}$ - $\frac{\sqrt{3}-1}{2}$=$\frac{3+\sqrt{3}}{2}$.在 Rt△CDN 中,由勾股定理,得 CD=$\sqrt{CN^2+DN^2}$=$\sqrt{(\frac{3-\sqrt{3}}{2})^2+(\frac{3+\sqrt{3}}{2})^2}$=$\sqrt{6}$.综上所述,CD 的长为 2 或$\sqrt{6}$.

7. 如图,已知点A(a,0)在x轴正半轴上,点B(0,b)在y轴正半轴上,$\triangle ABC$为等腰直角三角形,D为斜边BC的中点.若$OD= \sqrt{2}$,则$a+b= $2.

答案： 2 提示:过点 C 作 CE⊥x 轴于点 E,连接 AD,DE.根据题意,得∠OBA+∠BAO=90°,∠EAC+∠BAO=90°,所以∠OBA=∠EAC.在△ABO 和△CAE 中,$\left\{\begin{array}{l} ∠AOB=∠CEA,\\ ∠OBA=∠EAC,\\ AB=CA,\end{array}\right. $所以△ABO≌△CAE.所以 CE=AO=a,AE=BO=b.在 Rt△ABC 中,AB=AC,D 是斜边 BC 上的中点,所以 AD=CD,∠ABC=∠ACB=45°,∠ADB=∠ADC=90°.易知 OB//CE,所以∠OBC+∠ECD=180°.因为∠OBC+∠OAD=360° - ∠AOB - ∠ADB=180°,所以∠OAD=∠ECD.在△ADO 和△CDE 中,$\left\{\begin{array}{l} AO=CE,\\ ∠OAD=∠ECD,\\ AD=CD,\end{array}\right. $所以△ADO≌△CDE.所以 ED=OD=$\sqrt{2}$,∠ADO=∠CDE.因为∠ADE+∠CDE=90°,所以∠ADE+∠ADO=90°,即∠ODE=90°.在 Rt△ODE 中,根据勾股定理,得 OE=$\sqrt{OD^2+ED^2}$=2,所以 a+b=AO+AE=OE=2.

8. 如图,两条互相垂直的直线m,n交于点O,等腰直角三角形ABC的直角顶点A在直线m上,锐角顶点B在直线n上,D是斜边BC的中点.若$OD= \frac{5}{2}$,$BC= 4$,则$OA^{2}+OB^{2}= $8,$\triangle AOB$的面积为$\frac{9}{8}$.

答案： 8 $\frac{9}{8}$ 提示:因为 AC=AB,∠BAC=90°,BC=4,所以 AB²=8,所以 OA²+OB²=AB²=8.如图,过点 C 作 CE⊥直线 m 于点 E,连接 ED 并延长交直线 n 于点 F,则∠CEA=∠AOB=90°.设 OB=a,OA=b,所以 a²+b²=8,S△AOB=$\frac{1}{2}$OA·OB=$\frac{1}{2}$ab.因为∠BAC=90°,CA=AB,易证△CEA≌△AOB(AAS),所以 CE=AO=b,EA=OB=a,所以 OE=EA+OA=a + b.因为 CE⊥直线 m,BF⊥直线 m,所以∠F=∠CED,∠FDB=∠EDC.因为 D 是 BC 的中点,所以 BD=CD,所以△BDF≌△CDE(AAS),所以 BF=CE=b,DF=DE,所以 OF=OB+BF=a + b,所以 OE=OF,所以△OEF 是等腰直角三角形,所以 EF=2OD=5.在 Rt△OEF 中,由勾股定理,得 OE²+OF²=EF²,所以(a + b)²+(a + b)²=5²,所以(a + b)²=a²+b²+2ab=$\frac{25}{2}$.因为 a²+b²=8,所以 ab=$\frac{9}{4}$,所以 S△AOB=$\frac{1}{2}$ab=$\frac{9}{8}$.

9. 如图,在$Rt\triangle DEF$中,$\angle D= 90^{\circ}$,$DE= 3$,$DF= 4$,点A,B分别在边DE,DF上,将$\triangle DAB$沿直线AB折叠,使点D的对应点C恰好落在边EF上.若$\triangle DAB和\triangle DEF$中有一组锐角相等,则CE的长为$\frac{9}{5}$或$\frac{5}{2}$.

答案： $\frac{9}{5}$或$\frac{5}{2}$ 提示:在 Rt△DEF 中,DE=3,DF=4,所以 EF=5.根据题意分两种情况讨论:①如图 1,当∠DAB=∠E 时,AB//EF,由折叠的性质,可知 DC⊥AB,所以 DC⊥EF,从而 CD=$\frac{DF·DE}{EF}$=$\frac{12}{5}$,进而得 CE=$\sqrt{DE^2 - CD^2}$=$\frac{9}{5}$;②如图 2,当∠DAB=∠F 时,由折叠的性质,可知 DC⊥AB,所以∠EDC+∠DAB=90°,因为∠E+∠F=90°,所以∠EDC=∠E,所以 CE=CD,∠CDF=∠F,所以 CD=CF,所以 CE=CF=$\frac{1}{2}$EF=$\frac{5}{2}$.