《2025年小题狂做八年级数学上册苏科版巅峰版》

1. 某商店在节日期间开展优惠促销活动:购买原价超过 200 元的商品,超过 200 元的部分可以享受优惠.若购买商品的实际付款金额 y(元)与商品原价 x(元)之间的函数关系如图所示,则超过 200 元的部分可以享受的优惠是 (B)
A.打八折
B.打七折
C.打六折
D.打五折

答案： B 提示:设超过200元的部分可以享受的优惠是打n折.根据题意,得$y = 200 + (x - 200)×\frac{n}{10}$.当$x = 500$时,$y = 410$,即$410 = 200 + (500 - 200)×\frac{n}{10}$,解得$n = 7$.所以超过200元的部分可以享受的优惠是打七折.

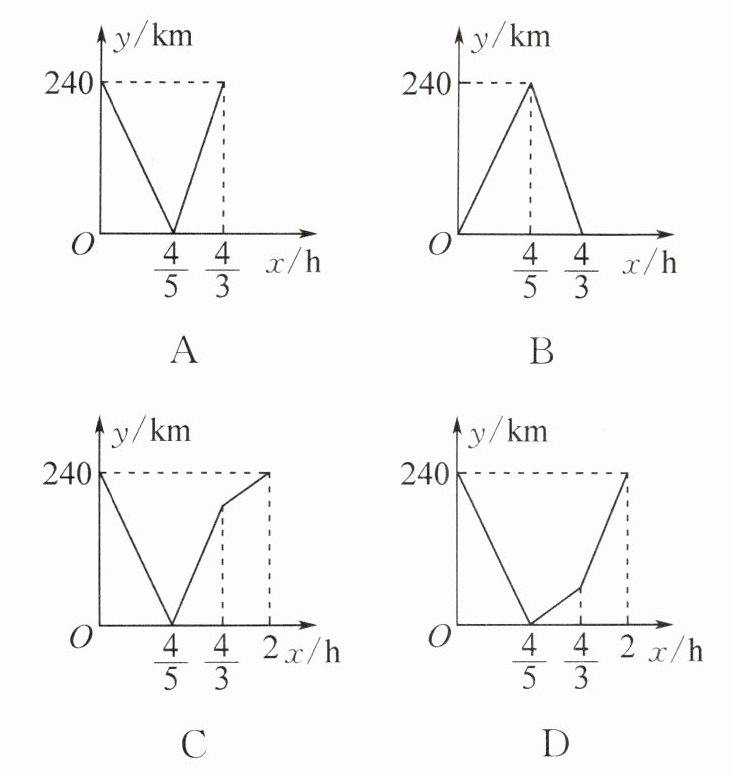
2. A,B 两地相距 240 km,慢车从 A 地到 B 地,快车从 B 地到 A 地,慢车的速度为 120 km/h,快车的速度为 180 km/h,两车同时出发.设两车的行驶时间为 x(h),两车之间的距离为 y(km).则能大致表示 y 与 x 之间函数关系的图象是 (C)

答案： C 提示:根据题意,得慢车从A地到B地所用的时间为$240÷120 = 2(h)$,快车从B地到A地所用的时间为$240÷180 = \frac{4}{3}(h)$.两车分别从A,B两地同时出发,即当$x = 0$时,$y = 240$;两车相遇即当$x = 240÷(120 + 180) = \frac{4}{5}$时,$y = 0$.当$0 ＜ x\leqslant\frac{4}{5}$时,$y = 240 - (120 + 180)x = 240 - 300x$;当$\frac{4}{5} ＜ x\leqslant\frac{4}{3}$时,$y = (120 + 180)(x - \frac{4}{5}) = 300x - 240$;当$\frac{4}{3} ＜ x\leqslant2$时,快车已到达A地,$y = 120x$.

3. 图1是甲、乙两个圆柱形水槽,一个圆柱形的空玻璃杯放置在乙槽中(空玻璃杯的厚度忽略不计).将甲槽的水匀速注入乙槽的空玻璃杯中,甲水槽内最高水位 y(cm)与注水时间 t(min)之间的函数关系如图2中线段 DE 所示,乙水槽(包括空玻璃杯)内最高水位 y(cm)与注水时间 t(min)之间的函数关系如图2中折线 O-A-B-C 所示.记甲槽底面积为$ S_1,$乙槽底面积为$ S_2,$乙槽中玻璃杯底面积为$ S_3,$则$ S_1:S_2:S_3 $的值为 (A)
A.4:5:2
B.4:5:3
C.8:5:1
D.8:10:5

答案： A 提示:由题意,可得$\begin{cases}10S_{1}=8S_{2}\\5S_{3}=\frac{2}{8}×10S_{1}\end{cases}$,所以$S_{1}:S_{2}:S_{3}=4:5:2$.

4. 甲、乙两辆汽车从同一出发地沿同一路线赶赴距出发地 480 km 的目的地,乙车比甲车晚 2 h 出发(从甲车出发时开始计时).图中折线 O-A-B-C、线段 DE 分别表示甲、乙两车所行路程 s(km)与时间 t(h)之间的函数关系(线段 AB 表示甲出发不足 2 h 时因故停车检修).根据图象所提供的信息,两车在途中第一次相遇时,乙车出发的时间为 ( B )
A.0.8 h
B.1 h
C.1.2 h
D.1.4 h

答案： B 提示:设乙车所行路程$s$与时间$t$之间的函数表达式为$s = k_{1}t + b_{1}(2\leqslant t\leqslant10)$.把点$(2,0)$,$(10,480)$代入,得$\begin{cases}2k_{1}+b_{1}=0\\10k_{1}+b_{1}=480\end{cases}$,解得$\begin{cases}k_{1}=60\\b_{1}=-120\end{cases}$,所以$s$与$t$之间的函数表达式为$s = 60t - 120$.交点F表示第二次相遇,点F的横坐标为6,此时$s = 60×6 - 120 = 240$,所以点F的坐标为$(6,240)$.设线段BC对应的函数关系式为$s = k_{2}t + b_{2}(4.5\leqslant t\leqslant8)$.把点$(6,240)$,$(8,480)$代入,得$\begin{cases}6k_{2}+b_{2}=240\\8k_{2}+b_{2}=480\end{cases}$,解得$\begin{cases}k_{2}=120\\b_{2}=-480\end{cases}$,所以线段BC对应的函数表达式为$s = 120t - 480$.所以当$t = 4.5$时,$s = 120×4.5 - 480 = 60$,所以点B的纵坐标为60.所以交点P的纵坐标为60.把$s = 60$代入$s = 60t - 120$,解得$t = 3$,所以交点P的坐标为$(3,60)$.因为交点P表示第一次相遇,所以乙车出发$3 - 2 = 1(h)$,两车在途中第一次相遇.