《2025年小题狂做八年级数学上册苏科版巅峰版》

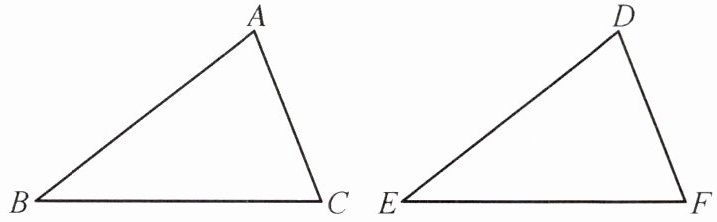
1. 如图,给出下列四组条件:①AB= DE,BC= EF,AC= DF;②AB= DE,∠B= ∠E,BC= EF;③∠B= ∠E,BC= EF,∠C= ∠F;④AB= DE,AC= DF,∠B= ∠E.其中能使△ABC≌△DEF的条件共有(C)

A.1组
B.2组
C.3组
D.4组

答案： C

2. (2024 南京市联合体期中)在△ABC和△A'B'C'中,AB= A'B',AC= A'C',∠B= ∠B'.下列条件不能确定△ABC≌△A'B'C'的是(B)
A.∠B= 90°
B.∠B＜∠C
C.∠B= ∠C
D.∠B＞∠C

答案： B

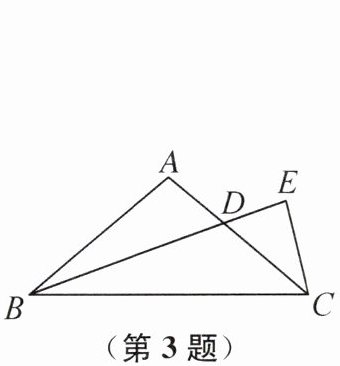
3. 如图,在△ABC中,∠ABC= ∠ACB= 40°,BD是△ABC的角平分线,延长BD至点E,使DE= AD,则∠ECA的度数为(C)

A.30°
B.35°
C.40°
D.45°

答案： C　提示:在BC上截取BF=AB,连接DF.因为∠ABC=∠ACB=40°,所以∠A=180°−∠ACB−∠ABC=100°,易证△ABD≌△FBD(SAS),所以DF=DA=DE,∠BFD=∠A=100°,所以∠CFD=180°−∠BFD=80°,所以∠FDC=180°−∠ACB−∠CFD=60°.因为BD是△ABC的角平分线,所以∠ABD= $\frac{1}{2}$∠ABC=20°.因为∠EDC=∠ADB=180°−∠ABD−∠A=60°,所以∠FDC=∠EDC.易证△DCE≌△DCF(SAS),所以∠ECA=∠ACB=40°.

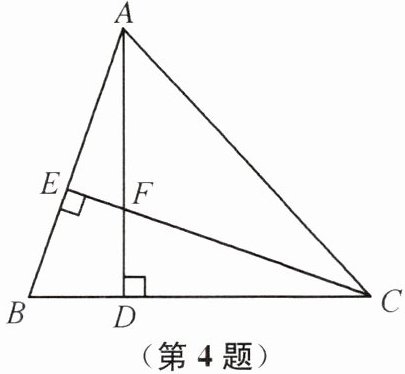
4. 如图,在△ABC中,AD⊥BC于点D,CE⊥AB于点E,AD与CE交于点F,且AD= CD.已知BC= 7,AD= 5,则AF的长为______.

3

答案： 3　提示:因为AD⊥BC,CE⊥AB,所以∠ADB=∠CDF=∠CEB=90°,所以∠BAD+∠B=∠FCD+∠B=90°,所以∠BAD=∠FCD.在△ABD和△CFD中,$\begin{cases} ∠ADB=∠CDF, \\ AD=CD, \\ ∠BAD=∠FCD, \end{cases}$所以△ABD≌△CFD.所以BD=FD.因为BC=7,CD=AD=5,所以FD=BD=BC−CD=2,所以AF=AD−FD=3.

5. 如图,在四边形ABCD中,AB= AD,∠BAD= ∠BCD= 90°,连接AC.若AC= 8,则四边形ABCD的面积为32.

答案： 32　提示:过点A作AE⊥AC,交CD的延长线于点E,则∠EAC=90°.因为∠BAD=90°,所以∠DAE+∠DAC=∠DAC+∠BAC=90°,所以∠DAE=∠BAC.因为∠BAD=∠BCD=90°,所以∠ADC+∠B=180°.因为∠EDA+∠ADC=180°,所以∠EDA=∠B.在△ABC和△ADE中,$\begin{cases} ∠BAC=∠DAE, \\ AB=AD, \\ ∠B=∠EDA, \end{cases}$所以△ABC≌△ADE,所以AE=AC=8,$S_{△ABC}=S_{△ADE}$.所以 $S_{四边形ABCD}=S_{△ACE}=\frac{1}{2}AC·AE=\frac{1}{2}×8×8=32$.

6. 如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE= DF,连接BF,CE,有下列说法:①△ABD和△ACD的面积相等;②∠BAD= ∠CAD;③△BDF≌△CDE;④BF//CE;⑤CE= BF.其中一定正确的有①③④⑤(填序号).

答案： ①③④⑤　提示:因为AD是△ABC的中线,所以BD=CD,所以△ABD和△ACD的面积相等,故①正确;无法证明∠BAD和∠CAD相等,故②错误;在△BDF和△CDE中,$\begin{cases} BD=CD, \\ ∠BDF=∠CDE, \\ DF=DE, \end{cases}$所以△BDF≌△CDE,故③正确;因为△BDF≌△CDE,所以∠F=∠DEC,所以BF//CE,故④正确;因为△BDF≌△CDE,所以CE=BF,故⑤正确.

7. 在△ABC中,∠C= 90°,AC= BC,分别过点A,B向过点C的直线CD作垂线,垂足分别为E,F.若AE= 3,BF= 1,则EF= ______.

答案：
4或2　提示:由∠C=∠BFC=∠CEA=90°,易证∠BCF=∠CAE.在△BFC和△CEA中,$\begin{cases} ∠BCF=∠CAE, \\ ∠BFC=∠CEA, \\ CB=AC, \end{cases}$所以△BFC≌△CEA,所以CF=AE=3,CE=BF=1.如图1,EF=CF+CE=4;如图2,EF=CF−CE=2. 　　

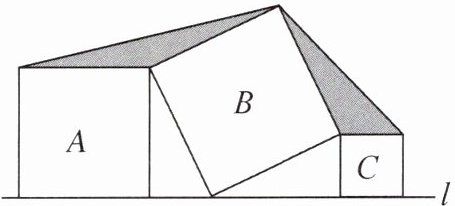
8. (2024 南京市校级期中)如图,在同一平面内,直线l同侧有三个正方形A,B,C.若A,C的面积分别为25和9,则阴影部分的总面积为______.

答案：
15　提示:如图,过点L作LM⊥FE,交FE的延长线于点M,交JI的延长线于点N.因为四边形A,B,C都是正方形,且正方形A,C的面积分别为25，9,所以DE=5,HI=3.易证△EDK≌△KHI(AAS),所以DK=HI=3,所以 $S_{△EDK}=S_{△KHI}=\frac{15}{2}$.因为∠LEM=90°−∠KEM=∠KED,所以易证△EML≌△EDK(AAS),所以EM=ED=EF,所以 $S_{△EFL}=S_{△EML}=S_{△EDK}=\frac{15}{2}$.同理△LNI≌△KHI(AAS),所以IN=IH=IJ,所以 $S_{△LJI}=S_{△LNI}=S_{△KHI}=\frac{15}{2}$.所以 $S_{△EFL}+S_{△LJI}=15$,即阴影部分的总面积为15. 　　　　

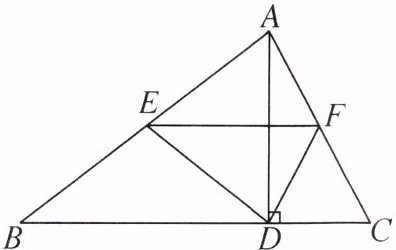
9. 如图,在△ABC中,AD是高,E,F分别是AB,AC的中点,AB= 8,AC= 6.
(1)求四边形AEDF的周长.
(2)若∠BAC= 90°,求四边形AEDF的面积.

答案： 解:
(1)延长DE至点G,使GE=DE,连接BG.在△AED和△BEG中,$\begin{cases} AE=BE, \\ ∠AED=∠BEG, \\ DE=GE, \end{cases}$所以△AED≌△BEG(SAS).所以AD=BG,∠DAE=∠GBE.因为AD⊥BC,所以∠DAE+∠ABD=90°.所以∠GBE+∠ABD=90°,即∠GBD=∠ADB=90°.在△GBD和△ADB中,$\begin{cases} BG=DA, \\ ∠GBD=∠ADB, \\ BD=DB, \end{cases}$所以△GBD≌△ADB(SAS).所以GD=AB.因为DE=$\frac{1}{2}$GD,所以DE=$\frac{1}{2}$AB=4.同理可证DF=$\frac{1}{2}$AC=3.所以四边形AEDF的周长为AE+ED+DF+FA=14.
(2)由
(1)得AE=DE=$\frac{1}{2}$AB=4,AF=DF=$\frac{1}{2}$AC=3,在△AEF和△DEF中,$\begin{cases} AE=DE, \\ AF=DF, \\ EF=EF, \end{cases}$所以△AEF≌△DEF(SSS).所以 $S_{△AEF}=S_{△DEF}$.因为∠BAC=90°,所以 $S_{△AEF}=\frac{1}{2}AE·AF=6$.所以 $S_{四边形AEDF}=S_{△AEF}+S_{△DEF}=2S_{△AEF}=12$.