第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 如图是由四个全等的直角三角形拼成的图形,设CE= a,HG= b,则斜边BD的长是(
A.a+b
B.a-b
C.$\sqrt{\frac{a^{2}+b^{2}}{2}}$
D.$\sqrt{\frac{a^{2}-b^{2}}{2}}$
C
)A.a+b
B.a-b
C.$\sqrt{\frac{a^{2}+b^{2}}{2}}$
D.$\sqrt{\frac{a^{2}-b^{2}}{2}}$
答案:
C 提示:根据题意,可设BC=DE=AG=x,CD=HA=y,所以$\begin{cases}x + y = a\\x - y = b\end{cases}$,解得$\begin{cases}x = \frac{a + b}{2}\\y = \frac{a - b}{2}\end{cases}$.所以$BC = \frac{a + b}{2}$,$CD = \frac{a - b}{2}$.在$Rt\triangle BCD$中,根据勾股定理,得$BD = \sqrt{BC^{2} + CD^{2}} = \sqrt{(\frac{a + b}{2})^{2} + (\frac{a - b}{2})^{2}} = \frac{\sqrt{a^{2} + b^{2}}}{2}$.
2. 如图,在平面直角坐标系中,△ABC≌△DEF,且AB= BC= 5. 若点A的坐标为(-3,1),B,C两点在直线y= -3上,D,E两点在y轴上,则点F到y轴的距离为(
A.2
B.3
C.4
D.5
C
)A.2
B.3
C.4
D.5
答案:
C
3. 我们把1,1,2,3,5,8,13,21,…这组数称为“斐波那契数列”,为了进一步研究,依次以这列数为半径作90°圆弧$\widehat{P_{1}P_{2}}$,$\widehat{P_{2}P_{3}}$,$\widehat{P_{3}P_{4}}$,…,得到斐波那契螺旋线,然后顺次连接P_1P_2,P_2P_3,P_3P_4,…,得到螺旋折线(如图),已知点P_1(0,1),P_2(-1,0),P_3(0,-1),则该折线上的点P_9的坐标为(
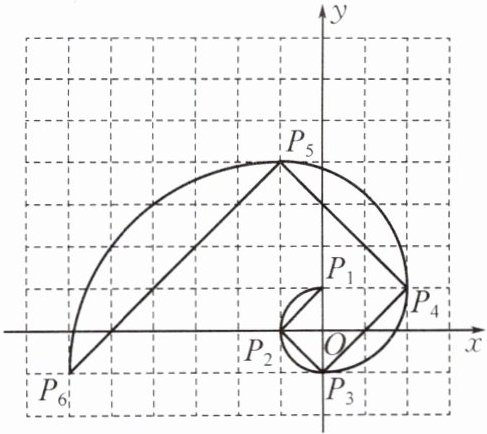
A.(-6,24)
B.(-6,25)
C.(-5,24)
D.(-5,25)
B
)
A.(-6,24)
B.(-6,25)
C.(-5,24)
D.(-5,25)
答案:
B
4. (2025无锡市宜兴市期末)如图,在Rt△ABC中,AB= BC,D是边AC上一动点,以BD为直角边,B为直角顶点作等腰直角三角形DBE,DE交BC于点F,连接CE. 过点B作BQ⊥DE于点P,交CD于点Q. 下面结论中正确的个数是(
①△ABD≌△CBE;②∠CDE= ∠ABD;③AD^2+CQ^2= DQ^2;④当AD:DC= 1:2时,S△BEC+S△DCE= $\frac{6}{5}$S△DBE;⑤当CE= CF时,AD:CD= $\sqrt{2}-1$.
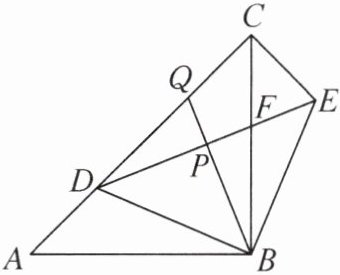
A.2
B.3
C.4
D.5
C
)①△ABD≌△CBE;②∠CDE= ∠ABD;③AD^2+CQ^2= DQ^2;④当AD:DC= 1:2时,S△BEC+S△DCE= $\frac{6}{5}$S△DBE;⑤当CE= CF时,AD:CD= $\sqrt{2}-1$.

A.2
B.3
C.4
D.5
答案:
C 提示:因为$\angle ABC = \angle DBE = 90^{\circ}$,所以$\angle ABD = \angle CBE$,所以$\triangle ABD \cong \triangle CBE(SAS)$,故①正确;因为$\angle ABC = 90^{\circ}$,$AB = BC$,所以$\angle A = \angle ACB = 45^{\circ}$,因为$\angle DBE = 90^{\circ}$,$DB = BE$,所以$\angle BDE = \angle BED = 45^{\circ}$,因为$\angle BDC = \angle A + \angle ABD = \angle BDE + \angle CDE$,所以$\angle ABD = \angle CDE$,故②正确;连接QE,因为$\angle DBE = 90^{\circ}$,$DB = BE$,$BQ \perp DE$,所以BQ垂直平分DE,所以$DQ = QE$,因为$\triangle ABD \cong \triangle CBE$,所以$\angle BCE = \angle A = 45^{\circ}$,$AD = CE$,所以$\angle QCE = 90^{\circ}$,所以$CQ^{2} + CE^{2} = QE^{2}$,所以$CQ^{2} + AD^{2} = DQ^{2}$,故③正确;因为$AD:DC = 1:2$,所以设$AD = a$,则$DC = 2a$,所以$AC = 3a$,所以$BC = AB = \frac{3\sqrt{2}}{2}a$,所以$DE = \sqrt{DC^{2} + CE^{2}} = \sqrt{5}a$,所以$BP = \frac{1}{2}DE = \frac{\sqrt{5}}{2}a$,所以$S_{\triangle DBE} = \frac{1}{2} \cdot \frac{\sqrt{5}}{2}a \cdot \sqrt{5}a = \frac{5}{4}a^{2}$,因为$S_{\triangle BEC} + S_{\triangle DCE} = \frac{1}{2} \cdot \frac{3\sqrt{2}}{2}a \cdot \frac{\sqrt{2}}{2}a + \frac{1}{2} \cdot a \cdot 2a = \frac{7}{4}a^{2}$,所以$S_{\triangle BEC} + S_{\triangle DCE} \neq \frac{6}{5}S_{\triangle DBE}$,故④错误;因为$CE = CF$,所以$\angle CFE = \angle CEF$,因为$\angle ECF = \angle BCD = \angle BDE = 45^{\circ}$,所以$\angle CEF = \angle CBD$,所以$\angle CDB = \angle CFE$,所以$\angle CDB = \angle CBD$,所以$CD = BC$,设$AB = BC = x = CD$,则$AC = \sqrt{2}x$,所以$AD = (\sqrt{2} - 1)x$,所以$AD:CD = \sqrt{2} - 1$,故⑤正确.
5. 如图,在△ABC中,∠ABC= 60°,BC= 6,AC= 8,点D,E在边AB,AC上,且AD= CE,则CD+BE的最小值为______
$2\sqrt{37}$
.
答案:
$2\sqrt{37}$ 提示:如图,作$CF // AB$,使$CF = AC$,作$BH \perp FC$,交FC的延长线于点H,连接EF,BF,则$\angle ECF = \angle A$,$\angle H = 90^{\circ}$,所以$\angle ABH = 180^{\circ} - \angle H = 90^{\circ}$.因为$\angle ABC = 60^{\circ}$,$BC = 6$,$AC = 8$,所以$\angle HBC = 30^{\circ}$,$CF = 8$,所以$CH = \frac{1}{2}BC = 3$,所以$FH = CF + CH = 8 + 3 = 11$,$BH^{2} = BC^{2} - CH^{2} = 6^{2} - 3^{2} = 27$,所以$BF = \sqrt{FH^{2} + BH^{2}} = \sqrt{11^{2} + 27} = 2\sqrt{37}$.在$\triangle EFC$和$\triangle DCA$中,$\begin{cases}CF = AC\\\angle ECF = \angle A\\CE = AD\end{cases}$,所以$\triangle EFC \cong \triangle DCA(SAS)$,所以$FE = CD$.因为$FE + BE \geq BF$,所以$CD + BE = FE + BE \geq 2\sqrt{37}$,当点E在线段BF上时取等号.所以$CD + BE$的最小值为$2\sqrt{37}$.
6. 如图,在四边形ABCD中,AD= 4,CD= 3,∠ABC= ∠ACB= ∠ADC= 45°,则BD的长为
$\sqrt{41}$
.
答案:
$\sqrt{41}$ 提示:如图,过点A作$AD' \perp AD$,垂足为A且$AD' = AD$,连接$CD'$,$DD'$.因为$\angle BAC + \angle CAD = \angle DAD' + \angle CAD$,所以$\angle BAD = \angle CAD'$.在$\triangle BAD$和$\triangle CAD'$中,$\begin{cases}BA = CA\\\angle BAD = \angle CAD'\\AD = AD'\end{cases}$,所以$\triangle BAD \cong \triangle CAD'$.所以$BD = CD'$.在$Rt\triangle ADD'$中,根据勾股定理,得$DD' = \sqrt{AD^{2} + (AD')^{2}} = 4\sqrt{2}$.又因为$\angle D'DA + \angle ADC = 90^{\circ}$,所以在$Rt\triangle CDD'$中,根据勾股定理,得$CD' = \sqrt{DC^{2} + (DD')^{2}} = \sqrt{41}$.所以$BD = CD' = \sqrt{41}$.
7. 如图,在△ABC中,AB= 4,AC= 7,M是BC的中点,AD平分∠BAC,过点M作MF//AD,交AC于点F,则CF的长为______.


5.5
答案:
5.5 提示:延长FM至点N,使$MN = MF$,连接BN,延长MF交BA延长线于点E.易证$\triangle BMN \cong \triangle CMF$,所以$BN = CF$,$\angle N = \angle CFM$.因为$MF // AD$,所以$\angle CAD = \angle CFM = \angle AFE = \angle N$,$\angle BAD = \angle E$.因为AD平分$\angle BAC$,所以$\angle BAD = \angle CAD = \angle AFE = \angle E = \angle N$,所以$AE = AF$,$BN = BE$,所以$CF = BN = BE = AB + AE = AB + AF = AB + AC - CF$,即$2CF = AB + AC$,所以$CF = \frac{1}{2}(AB + AC) = 5.5$.
查看更多完整答案,请扫码查看


