《2025年小题狂做八年级数学上册苏科版巅峰版》

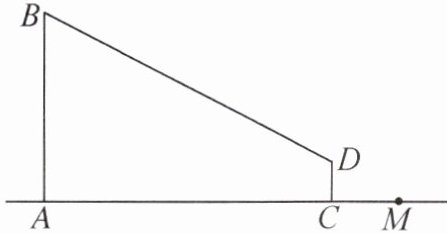
8. 一天傍晚,小方和家人去小区遛狗,小方观察发现,她站直身体时,牵绳的手离地面高度为AB= 1.3m,小狗的高CD= 0.3m,小狗与小方的距离AC= 2.4m(绳子一直是直的).
(1)求此时牵狗绳BD的长.
(2)小方将手上的小球扔至3m远的点M处,若她站着不动,牵狗绳最长放至4m,则小狗能否将小球捡回来？请说明理由(假设小狗碰到球就能将球捡回来).

答案：
解：（1）如图1，过点D作DE⊥AB于点E，则AE=CD=0.3m，DE=AC=2.4m，所以BE=AB - AE=1m，所以BD=√(BE²+DE²)=2.6m.所以此时牵狗绳BD的长为2.6m.

（2）如图2，过点M作MN⊥AM，交ED的延长线于点N，连接BN.由（1）得BE=1.因为NE=AM=3m，所以BN=√(BE²+NE²)=√10m.因为√10＜4，所以小狗能将小球捡回来.

9. 对于正数a,b,c,d,如果a+b= c+d,试比较$\sqrt{a^{2}+c^{2}}+\sqrt{b^{2}+d^{2}}与\sqrt{2(a+b)^{2}}$的大小.

答案：
解：如图，在正方形ABCD中，BF=√(a²+c²)，DF=√(b²+d²)，BD=√[2(a+b)²].根据三角形两边之和大于第三边，得√(a²+c²)+√(b²+d²)＞√[2(a+b)²].当点F在BD上时，即b=d，a=c时，√(a²+c²)+√(b²+d²)=√[2(a+b)²].综上所述，√(a²+c²)+√(b²+d²)≥√[2(a+b)²].

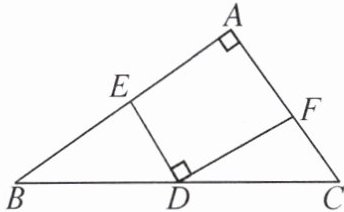
10. 如图,在Rt△ABC中,∠A= 90°,D为斜边BC的中点,DE⊥DF,求证：$EF^{2}= BE^{2}+CF^{2}$.

答案：
证明：如图，延长ED至点G，使DG=DE，连接EF，FG，CG.在△EDF和△GDF中，{DF = DF，∠EDF = ∠FDG，DE = DG}，所以△EDF≌△GDF(SAS)，所以EF=GF.因为D为斜边BC的中点，所以BD=DC.在△BDE和△CDG中，{BD = DC，∠BDE = ∠CDG，DE = DG}，所以△BDE≌△CDG(SAS).所以BE=CG，∠B=∠BCG.所以AB//CG，所以∠GCA=180° - ∠A=90°.在Rt△FCG中，由勾股定理，得GF²=CG²+CF²=BE²+CF².所以EF²=BE²+CF².