第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
9. 如图,在$Rt\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AC= BC$,$P是\triangle ABC$内部一点,且$\angle APB= \angle BPC= 135^{\circ}$,则$PA与PC$的数量关系为______

PA=2PC
.
答案:
PA=2PC 提示:在线段AP上取点D,使得AD=CP,连接CD.因为∠APB=∠BPC=135°,所以∠APC=360°-∠APB-∠BPC=90°,∠ABP+∠PAB=180°-∠APB=45°,∠CBP+∠BCP=180°-∠BPC=45°.在Rt△ABC中,∠ACB=90°,AC=BC,所以∠CAB=∠CBA=45°,所以∠CAP+∠PAB=45°,∠ABP+∠CBP=45°,所以∠CAD=∠ABP=∠BCP,易证△ADC≌△CPB(SAS),所以∠ADC=∠CPB=135°,所以∠PDC=45°,所以△CPD是等腰直角三角形,所以CP=DP.因为PA=AD+DP,所以PA=2PC.
10. $A,B,C$三地依次在同一直线上,甲、乙两人同时从$A地出发前往C$地,已知当甲行走到$B$地时发现有重要物品放在乙处,于是甲立即返回与乙相遇,相遇以后甲、乙继续前往$C$地,最终甲比乙提前8min到达$C$地.若中途停留的时间忽略不计,且在整个行走过程中,甲、乙均保持各自速度匀速行走,甲、乙两人之间的距离$y(m)与乙行走的时间x(min)$之间的函数关系如图所示,则$B,C$两地的距离为______m.


990
答案:
990 提示:设甲的速度为a m/min,乙的速度为b m/min.由题图象可得{5(a-b)=110,a+b=110,解得{a=66,b=44.设BC=s m,则相遇地点到C地的距离为(s+66)m.由题意,得(s+66)/44-(s+66)/66=8,解得s=990.所以B,C两地的距离为990 m.
11. (2025泰州市泰兴市期末)如图1,在$Rt\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AC= BC= 4$,$P是AB$的中点,$E,F分别是边AC,BC$上的动点,连接$PE,PF$,将$\triangle APE$,$\triangle BPF分别沿着PE,PF$翻折,点$A和点B的对应点都是Q$.
(1)$\angle EQF= $______°,$CE+CF= $______.
(2)如图2,当$AE= 1$时,求点$Q到AC$的距离.
(3)连接$CQ,EF$,试探究$CQ与EF$的位置关系,并证明.
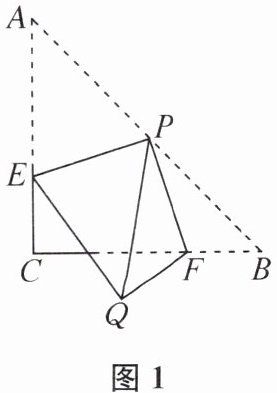
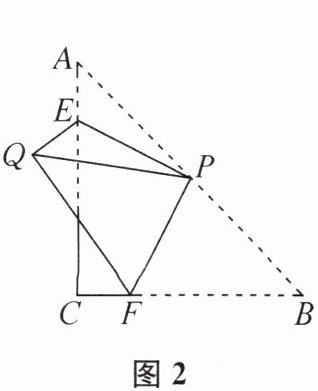
(1)$\angle EQF= $______°,$CE+CF= $______.
(2)如图2,当$AE= 1$时,求点$Q到AC$的距离.
(3)连接$CQ,EF$,试探究$CQ与EF$的位置关系,并证明.


答案:
(1) 90 4 提示:因为∠EQP=∠BAC,∠FQP=∠ABC,所以∠EQF=∠EQP+∠FQP=∠BAC+∠ABC=90°.如图1,连接PC.因为∠EPC=90°-∠CPF=∠FPB,∠ECP=∠B=45°,PC=PB,所以△PCE≌△PBF(ASA),所以CE=BF,所以CE+CF=BF+CF=BC=4.

(2) 如图2,连接PC,过点Q作QH⊥AC于点H.设QF,AC交于点G,同
(1)可证△PCE≌△PBF,所以CE=BF,同理CE+CF=BF+CF=CB=4.因为AE=AC-CE=BC-BF=CF,AE=QE,所以CF=QE,在△FGC和△EGQ中,{∠FCG=∠EQG,∠FGC=∠EGQ,CF=QE,所以△FGC≌△EGQ(AAS),所以CG=QG,FG=EG.设CG=x,则GF=GE=3-x.在Rt△FGC中,由勾股定理,得CG²+CF²=GF²,即x²+1²=(3-x)²,解得x=4/3.所以QG=CG=4/3,GF=GE=5/3.在Rt△EQG中,QE·QG=EG·QH,所以QH=4/5.

(3) CQ//EF.证明如下:
设QF与AC交于点G.由
(2),得△FGC≌△EGQ,所以CG=QG,FG=EG,所以∠GQC=∠GCQ=(180°-∠QGC)/2,∠GEF=∠GFE=(180°-∠EGF)/2.因为∠QGC=∠EGF,所以∠GQC=∠GFE,所以CQ//EF.
(1) 90 4 提示:因为∠EQP=∠BAC,∠FQP=∠ABC,所以∠EQF=∠EQP+∠FQP=∠BAC+∠ABC=90°.如图1,连接PC.因为∠EPC=90°-∠CPF=∠FPB,∠ECP=∠B=45°,PC=PB,所以△PCE≌△PBF(ASA),所以CE=BF,所以CE+CF=BF+CF=BC=4.

(2) 如图2,连接PC,过点Q作QH⊥AC于点H.设QF,AC交于点G,同
(1)可证△PCE≌△PBF,所以CE=BF,同理CE+CF=BF+CF=CB=4.因为AE=AC-CE=BC-BF=CF,AE=QE,所以CF=QE,在△FGC和△EGQ中,{∠FCG=∠EQG,∠FGC=∠EGQ,CF=QE,所以△FGC≌△EGQ(AAS),所以CG=QG,FG=EG.设CG=x,则GF=GE=3-x.在Rt△FGC中,由勾股定理,得CG²+CF²=GF²,即x²+1²=(3-x)²,解得x=4/3.所以QG=CG=4/3,GF=GE=5/3.在Rt△EQG中,QE·QG=EG·QH,所以QH=4/5.

(3) CQ//EF.证明如下:
设QF与AC交于点G.由
(2),得△FGC≌△EGQ,所以CG=QG,FG=EG,所以∠GQC=∠GCQ=(180°-∠QGC)/2,∠GEF=∠GFE=(180°-∠EGF)/2.因为∠QGC=∠EGF,所以∠GQC=∠GFE,所以CQ//EF.
12. (2025盐城市盐都区期末)如图,直线$l_{1}:y= -x+2与x$轴、$y轴分别交于点A,B$,另一直线$l_{2}:y= \frac{4}{3}x+b与x$轴、$y轴分别交于点C,D$,连接$AD$.直线$l_{1}与直线l_{2}交于点E(-3,m)$,在$x轴上有一点P(a,0)(a<-3)$,过点$P作x$轴的垂线,分别与直线$l_{1},l_{2}交于点M,N$.
(1)求$m的值及\triangle ABD$的面积.
(2)若$MN= BD$,求$a$的值.
(3)在$y轴上找点Q$,使得$\triangle DEQ$为等腰三角形,求点$Q$的坐标.
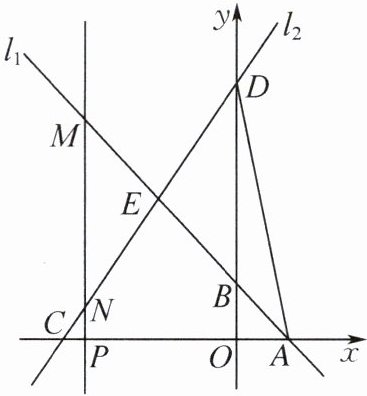
(1)求$m的值及\triangle ABD$的面积.
(2)若$MN= BD$,求$a$的值.
(3)在$y轴上找点Q$,使得$\triangle DEQ$为等腰三角形,求点$Q$的坐标.

答案:
(1) 因为直线l₁:y=-x+2与另一直线l₂:y=4/3x+b交于点E(-3,m),所以m=-(-3)+2=5,即点E(-3,5).把点E的坐标代入l₂:y=4/3x+b,得5=4/3×(-3)+b,解得b=9,所以直线l₂:y=4/3x+9.因为点A(2,0),B(0,2),D(0,9),所以BD=9-2=7,所以S△ABD=1/2BD·xA=1/2×7×2=7.
(2) 因为点P(a,0),所以点M(a,-a+2),N(a,4/3a+9).因为MN=BD,所以-a+2-(4/3a+9)=7,所以a=-6.
(3) 过点E作EF⊥y轴于点F.因为点E(-3,5),所以OF=5,EF=3.因为点D(0,9),所以DF=9-5=4.在Rt△DEF中,由勾股定理,得DE=√(EF²+DF²)=√(3²+4²)=5.如图1,若DE为腰,则DQ₁=DQ₂=DE=5,DF=FQ₃=4.所以点Q₁(0,14),Q₂(0,4),Q₃(0,1);如图2,若DE为底,则DE的垂直平分线交y轴于点Q₄,所以EQ₄=DQ₄,设FQ₄=x,则EQ₄=DQ₄=4-x,在Rt△EFQ₄中,由勾股定理,得3²+x²=(4-x)²,解得x=7/8,所以OQ₄=OF+FQ₄=5+7/8=47/8,所以点Q₄(0,47/8).综上所述,点Q的坐标为(0,14)或(0,4)或(0,1)或(0,47/8).


(1) 因为直线l₁:y=-x+2与另一直线l₂:y=4/3x+b交于点E(-3,m),所以m=-(-3)+2=5,即点E(-3,5).把点E的坐标代入l₂:y=4/3x+b,得5=4/3×(-3)+b,解得b=9,所以直线l₂:y=4/3x+9.因为点A(2,0),B(0,2),D(0,9),所以BD=9-2=7,所以S△ABD=1/2BD·xA=1/2×7×2=7.
(2) 因为点P(a,0),所以点M(a,-a+2),N(a,4/3a+9).因为MN=BD,所以-a+2-(4/3a+9)=7,所以a=-6.
(3) 过点E作EF⊥y轴于点F.因为点E(-3,5),所以OF=5,EF=3.因为点D(0,9),所以DF=9-5=4.在Rt△DEF中,由勾股定理,得DE=√(EF²+DF²)=√(3²+4²)=5.如图1,若DE为腰,则DQ₁=DQ₂=DE=5,DF=FQ₃=4.所以点Q₁(0,14),Q₂(0,4),Q₃(0,1);如图2,若DE为底,则DE的垂直平分线交y轴于点Q₄,所以EQ₄=DQ₄,设FQ₄=x,则EQ₄=DQ₄=4-x,在Rt△EFQ₄中,由勾股定理,得3²+x²=(4-x)²,解得x=7/8,所以OQ₄=OF+FQ₄=5+7/8=47/8,所以点Q₄(0,47/8).综上所述,点Q的坐标为(0,14)或(0,4)或(0,1)或(0,47/8).


查看更多完整答案,请扫码查看


