《2025年通城学典暑期升级训练延边大学出版社小升初衔接数学》

1. 计算$(-1)^{2021}$的结果是 (B)
A.1
B.-1
C.2021
D.-2021

答案： B

2. 下列各式中,计算正确的是 (C)
A.$-3^{2}= (-3)^{2}$
B.$-1^{4}= (-1)^{4}$
C.$(-2)^{3}= -2^{3}$
D.$(-1)^{3}= -3$

答案： C 解析:$-3^{2}=-9$,$(-3)^{2}=9$,故A选项错误;$-1^{4}=-1$,$(-1)^{4}=1$,故B选项错误;$(-2)^{3}=-8$,$-2^{3}=-8$,故C选项正确;$(-1)^{3}=-1$,故D选项错误.

3. 计算$-5^{2}$的结果是 (D)
A.10
B.-10
C.25
D.-25

答案： D

4. 下列各组数中,互为相反数的是 (D)
A.$-|-2|和+(-2)$
B.$+(-6)和-(+6)$
C.$(-4)^{3}和-4^{3}$
D.$(-5)^{2}和-5^{2}$

答案： D

5. 在$-(-6),|-3|,3^{2},(-1)^{3}$这四个数中,负数有 (A)
A.4个
B.3个
C.2个
D.1个

答案： A

6. 下列各式中,计算正确的是 (A)
A.$+2^{2}= 4$
B.$(-2)^{3}= -6$
C.$(-3)^{2}= 6$
D.$(-1)^{2}= -1$

答案： 解析：本题可根据有理数的乘方运算法则，分别对选项中的式子进行计算，再判断其计算是否正确。
有理数的乘方是指求$n$个相同因数乘积的运算，记作$a^n$，其中$a$叫做底数，$n$叫做指数。当$n$为正整数时，$a^n$表示$n$个$a$相乘。
选项A：计算$+2^{2}$的值
根据运算顺序，先计算指数运算，再考虑符号。$2^{2}$表示$2$个$2$相乘，即$2^{2}=2×2 = 4$，所以$+2^{2}=4$，该选项计算正确。
选项B：计算$(-2)^{3}$的值
$(-2)^{3}$表示$3$个$-2$相乘，即$(-2)^{3}=(-2)×(-2)×(-2)=4×(-2)= - 8\neq - 6$，该选项计算错误。
选项C：计算$(-3)^{2}$的值
$(-3)^{2}$表示$2$个$-3$相乘，即$(-3)^{2}=(-3)×(-3)= 9\neq 6$，该选项计算错误。
选项D：计算$(-1)^{2}$的值
$(-1)^{2}$表示$2$个$-1$相乘，即$(-1)^{2}=(-1)×(-1)= 1\neq - 1$，该选项计算错误。
答案：A。

7. 不大于$(-\frac{3}{2})^{3}$的最大整数是 (A)
A.-4
B.-3
C.3
D.4

答案： A 解析:$\left(-\frac{3}{2}\right)^{3}=-\frac{27}{8}=-3\frac{3}{8}$,在不大于$-3\frac{3}{8}$ 的整数中,$-4$是最大的.

8. 立方后结果为-125的数是 (B)
A.5
B.-5
C.25
D.-25

答案： B

9. $-2^{4}$中的底数是2,指数是4.

答案： 2 4

10. $\pm\frac{4}{3}$的平方是$\frac{16}{9}$;$\frac{3}{2}$的立方是$\frac{27}{8}$.

答案： $\pm\frac{4}{3}$ $\frac{3}{2}$

11. $0^{2}= $0.

答案： 0

12. $(-\frac{2}{3})^{3}=$$-\frac{8}{27}$.

答案： $-\frac{8}{27}$

13. $1^{101}= $1.

答案： 1

14. 计算:$-(-1)^{2022}+2= $1.

答案： 解析：
首先计算$(-1)^{2022}$，由于$-1$的偶数次方等于$1$，所以$(-1)^{2022} = 1$。
然后，计算$-(-1)^{2022}$，即$-1$。
最后，进行加法运算，$-1 + 2 = 1$。
答案：
$1$

15. 计算:
(1)$5^{3}$; (2)$(-0.1)^{2}$;
(3)$(-\frac{1}{3})^{2}$; (4)$-(-5)^{3}$;
(5)$(-1)^{3}×(-0.2)^{2}$;
(6)$-(+7)^{2}$.

答案： （1）125 （2）$\frac{1}{100}$ （3）$\frac{1}{9}$ （4）125（5）$-\frac{1}{25}$ （6）$-49$

16. 若$-(-2)^{4}= a,(-3)^{3}= b$,求$(a-b)^{2}$的值.

答案： 因为$-(-2)^{4}=-16$,所以$a=-16$.因为$(-3)^{3}=-27$,所以$b=-27$.所以$(a-b)^{2}=[-16-(-27)]^{2}=(-16+27)^{2}=11^{2}=121$

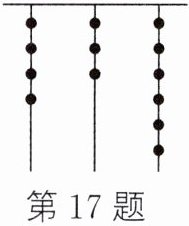
17. 远古时期,人们通过在绳子上打结来记录数量,即"结绳记数".如图,一位母亲在从右到左依次排列的绳子上打结,满七进一,用来记录孩子自出生后的天数.孩子自出生后是多少天?

答案： $4×7^{2}+3×7+6=223$(天）解析:类比于现在的十进制“满十进一”,可以表示“满七进一”的数:百位上的数$×7^{2}+$十位上的数$×7+$个位上的数.