第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 小鸭擅长游泳,在岸上行走却很吃力。它想从点A到河对岸的点B去,请帮它设计一条最省力的路线,在图中画出该路线。
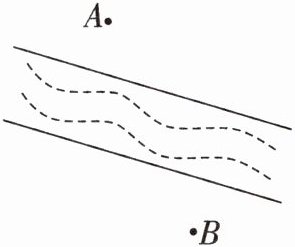

答案:


2. 如图,若猫在现在的位置不动,则请画出小老鼠不会被猫看见的活动区域,并画上阴影。


答案:


1. 一间房子的占地形状是长方形,长6米,宽4米,房子四周是草地。王爷爷将一只羊拴在房子的外墙角处(紧靠地面,如图),拴羊的绳子长6米。
(1)在下图中画出这只羊能吃到草的范围,并将范围内的草地画上阴影。
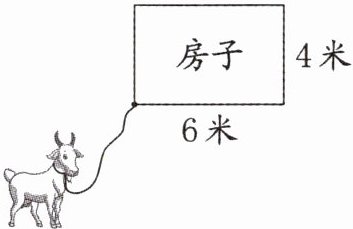
(2)求这只羊能吃到草的草地面积。
(1)在下图中画出这只羊能吃到草的范围,并将范围内的草地画上阴影。

(2)求这只羊能吃到草的草地面积。
答案:
(1)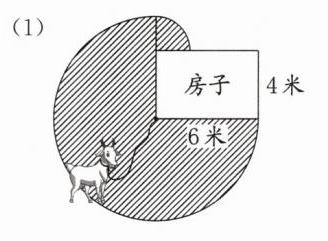
(2) 羊能吃到草的面积由两部分组成:
以6米为半径的3/4圆面积:$ \frac{3}{4} × \pi × 6^2 = \frac{3}{4} × 3.14 × 36 = 84.78 $(平方米)
绳子超出房子宽的部分为$ 6 - 4 = 2 $米,以2米为半径的1/4圆面积:$ \frac{1}{4} × \pi × 2^2 = \frac{1}{4} × 3.14 × 4 = 3.14 $(平方米)
总面积:$ 84.78 + 3.14 = 87.92 $(平方米)
答:这只羊能吃到草的草地面积是87.92平方米。
(1)

(2) 羊能吃到草的面积由两部分组成:
以6米为半径的3/4圆面积:$ \frac{3}{4} × \pi × 6^2 = \frac{3}{4} × 3.14 × 36 = 84.78 $(平方米)
绳子超出房子宽的部分为$ 6 - 4 = 2 $米,以2米为半径的1/4圆面积:$ \frac{1}{4} × \pi × 2^2 = \frac{1}{4} × 3.14 × 4 = 3.14 $(平方米)
总面积:$ 84.78 + 3.14 = 87.92 $(平方米)
答:这只羊能吃到草的草地面积是87.92平方米。
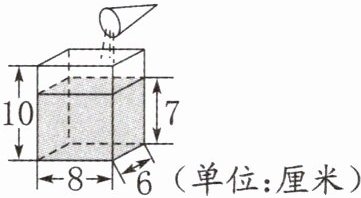
2. (常州溧阳)一个数学实验小组的4名同学进行下面的数学实验。
丁丁:一个圆锥形玻璃容器从里面量底面半径是2厘米,高是6厘米。
东东:我用沙装满这个圆锥形玻璃容器。
西西:一个长方体玻璃容器从里面量长是8厘米,宽是6厘米,高是10厘米。我已在这个长方体玻璃容器中装了沙,沙的厚度为7厘米。
星星:把东东装的沙全部倒入这个装有一部分沙的长方体玻璃容器中。
根据他们的实验解决问题。(π取3)
(1)东东是用多少立方厘米的沙装满这个圆锥形玻璃容器的?
(2)星星把东东装的沙全部倒入装有一部分沙的长方体玻璃容器后,倒入的沙与玻璃接触部分的面积是多少平方厘米?
丁丁:一个圆锥形玻璃容器从里面量底面半径是2厘米,高是6厘米。
东东:我用沙装满这个圆锥形玻璃容器。
西西:一个长方体玻璃容器从里面量长是8厘米,宽是6厘米,高是10厘米。我已在这个长方体玻璃容器中装了沙,沙的厚度为7厘米。
星星:把东东装的沙全部倒入这个装有一部分沙的长方体玻璃容器中。
根据他们的实验解决问题。(π取3)
(1)东东是用多少立方厘米的沙装满这个圆锥形玻璃容器的?
(2)星星把东东装的沙全部倒入装有一部分沙的长方体玻璃容器后,倒入的沙与玻璃接触部分的面积是多少平方厘米?

答案:
(1)圆锥体积公式:$V=\frac{1}{3}\pi r^2h$,其中$r=2$厘米,$h=6$厘米,$\pi=3$。
$\begin{aligned}V&=\frac{1}{3}×3×2^2×6\\&=\frac{1}{3}×3×4×6\\&=1×4×6\\&=24\end{aligned}$
答:东东用了24立方厘米的沙。
(2)长方体容器底面积:$8×6=48$平方厘米。
倒入沙的高度:$24÷48=0.5$厘米。
此时沙的总高度:$7 + 0.5=7.5$厘米。
倒入的沙与玻璃接触部分为长方体四周侧面(不含上表面),面积为:
$\begin{aligned}&2×(8×7.5 + 6×7.5)\\=&2×7.5×(8 + 6)\\=&15×14\\=&210\end{aligned}$
答:倒入的沙与玻璃接触部分的面积是210平方厘米。
(1)圆锥体积公式:$V=\frac{1}{3}\pi r^2h$,其中$r=2$厘米,$h=6$厘米,$\pi=3$。
$\begin{aligned}V&=\frac{1}{3}×3×2^2×6\\&=\frac{1}{3}×3×4×6\\&=1×4×6\\&=24\end{aligned}$
答:东东用了24立方厘米的沙。
(2)长方体容器底面积:$8×6=48$平方厘米。
倒入沙的高度:$24÷48=0.5$厘米。
此时沙的总高度:$7 + 0.5=7.5$厘米。
倒入的沙与玻璃接触部分为长方体四周侧面(不含上表面),面积为:
$\begin{aligned}&2×(8×7.5 + 6×7.5)\\=&2×7.5×(8 + 6)\\=&15×14\\=&210\end{aligned}$
答:倒入的沙与玻璃接触部分的面积是210平方厘米。
3. (宁波镇海区)小东利用两种方法测量石块的体积。
方法一:利用盛水的容器。
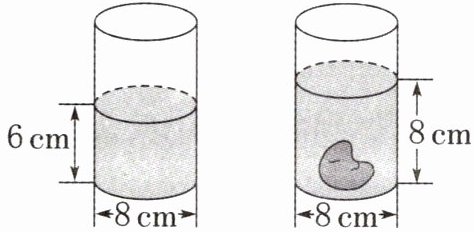
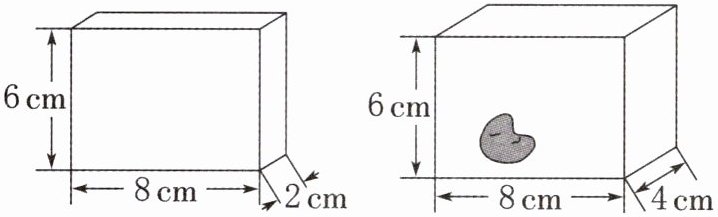
方法二:利用橡皮泥。
(1)这两种方法相同的地方是(
(2)请选择一种方法计算石块的体积。(π取3)
选择方法一:
容器底面半径:8÷2=4(cm)
水面上升高度:8-6=2(cm)
石块体积:3×4²×2=3×16×2=96(cm³)
答:石块的体积是96cm³。
或选择方法二:
橡皮泥初始体积:8×2×6=96(cm³)
放入石块后橡皮泥体积:8×4×6=192(cm³)
石块体积:192-96=96(cm³)
答:石块的体积是96cm³。
方法一:利用盛水的容器。

方法二:利用橡皮泥。

(1)这两种方法相同的地方是(
都利用了排水法(或都通过测量排开的液体/物体的体积来求石块体积)
)。(2)请选择一种方法计算石块的体积。(π取3)
选择方法一:
容器底面半径:8÷2=4(cm)
水面上升高度:8-6=2(cm)
石块体积:3×4²×2=3×16×2=96(cm³)
答:石块的体积是96cm³。
或选择方法二:
橡皮泥初始体积:8×2×6=96(cm³)
放入石块后橡皮泥体积:8×4×6=192(cm³)
石块体积:192-96=96(cm³)
答:石块的体积是96cm³。
答案:
(1)都利用了排水法(或都通过测量排开的液体/物体的体积来求石块体积)
(2)选择方法一:
容器底面半径:8÷2=4(cm)
水面上升高度:8-6=2(cm)
石块体积:3×4²×2=3×16×2=96(cm³)
答:石块的体积是96cm³。
或选择方法二:
橡皮泥初始体积:8×2×6=96(cm³)
放入石块后橡皮泥体积:8×4×6=192(cm³)
石块体积:192-96=96(cm³)
答:石块的体积是96cm³。
(1)都利用了排水法(或都通过测量排开的液体/物体的体积来求石块体积)
(2)选择方法一:
容器底面半径:8÷2=4(cm)
水面上升高度:8-6=2(cm)
石块体积:3×4²×2=3×16×2=96(cm³)
答:石块的体积是96cm³。
或选择方法二:
橡皮泥初始体积:8×2×6=96(cm³)
放入石块后橡皮泥体积:8×4×6=192(cm³)
石块体积:192-96=96(cm³)
答:石块的体积是96cm³。
查看更多完整答案,请扫码查看


