《2025年暑假作业河北美术出版社七年级数学人教版》

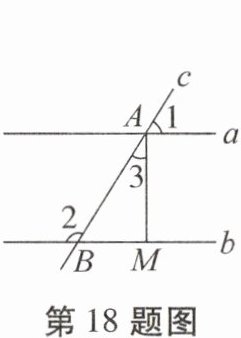
18. 如图,直线$a// b$,直线c与直线a,b分别相交于点A,B,$∠1= 58^{\circ }$.
(1)$∠2$的度数是$58^{\circ }$;
(2)若$AM⊥b$,垂足是M,则$∠3$的度数是$32^{\circ }$.

答案： 18.
(1)$58^{\circ}$
(2)$32^{\circ}$

19. 如图,在平面直角坐标系中,$AB// EG// x$轴,$BC// DE// HG// AP// y$轴,点D,C,P,H在x轴上,$A(1,2),B(-1,2),D(-3,0),E(-3,-2),G(3,-2)$.

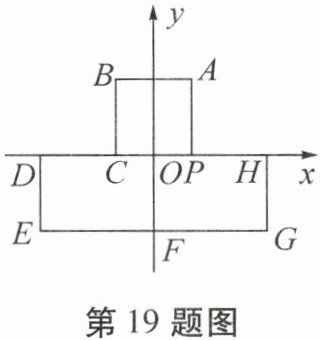
(1)若点M在线段EG上,当点M与点A的距离最小时,点M的坐标是$(1,-2)$;
(2)把一条长是202个单位长度且无弹性的细线(粗细忽略不计)的一端固定在A处,并按$A→B→C→D→E→F→G→H→P→A... ... $的规律紧绕在图形“凸”的边上,则细线的另一端所在位置的点的坐标是$(-1,2)$.

答案： 19.
(1)$(1,-2)$
(2)$(-1,2)$

三、解答题
20. 按要求完成下列各小题.
(1)计算:$(-1)^{201}+\sqrt [3]{-8}+\sqrt {9}=$0;
(2)解方程组:$\left\{\begin{array}{l} 2x-y= 7,\\ 4x+y= 5.\end{array} \right. $
解:$\begin{cases}2x - y = 7①\\4x + y = 5②\end{cases}$
$① + ②$,得$6x = 12$. 解得$x = 2$. 把$x = 2$代入$①$,得$2×2 - y = 7$. 解得$y = -3$. ∴原方程组的解是$\begin{cases}x = 2\\y = -3\end{cases}$

答案： 20.
(1)原式$=-1-2+3=0$.
(2)$\begin{cases}2x - y = 7①\\4x + y = 5②\end{cases}$
$① + ②$,得$6x = 12$. 解得$x = 2$. 把$x = 2$代入$①$,得$2×2 - y = 7$. 解得$y = -3$.
∴原方程组的解是$\begin{cases}x = 2\\y = -3\end{cases}$.

21. 整式$5(m-\frac {1}{5})$的值是P.
(1)当$m= 3$时,求P的值;14
(2)若P的取值范围如图所示,求m的正整数值.1,2

答案： 21.
(1)根据题意,得$P = 5×(3 - \frac{1}{5}) = 14$.
(2)根据题意,得$5(m - \frac{1}{5}) ≤ 9$. 解得$m ≤ 2$.
∴$m$的正整数值是1,2.

22. 某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己最喜欢的一个版面,将调查数据进行了整理,绘制成如图所示的两幅统计图(不完整).

(1)这次被调查的学生有50人,“第一版”对应扇形的圆心角是108°;
(2)请补全条形图;
(3)若该校有1200名学生,请你估计全校学生中最喜欢“第三版”的人数.

答案：
22.
(1)50 108
(2)最喜欢“第三版”的人数为$50 - 15 - 5 - 18 = 12$,补全的条形图如答图.
(3)$1200×\frac{12}{50} = 288$.
∴估计全校学生中最喜欢“第三版”的人数是288.