《2025年暑假作业河北美术出版社七年级数学人教版》

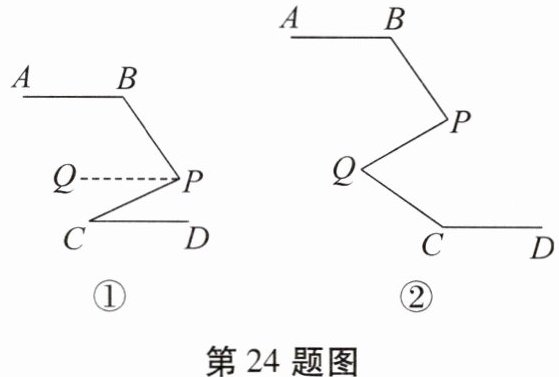
24. 数学活动课上,老师把山路抽象成如图①所示的图形,并提出了一个问题:如图①,$AB// CD,∠B= 125^{\circ },∠C= 25^{\circ }$,求$∠BPC$的度数.
嘉嘉的解法如下.
解:如图①,过点P作$PQ// AB.$
$\because AB// CD,$
$\therefore PQ// CD$(依据1).
$\therefore ∠CPQ= ∠C= 25^{\circ }.$
$\because AB// PQ,$
$\therefore ∠B+∠BPQ= 180^{\circ }$(依据2).
……

(1)嘉嘉的解法中的依据1是平行于同一条直线的两条直线平行,依据2是两直线平行，同旁内角互补;
(2)按照上面嘉嘉的解题思路,完成嘉嘉剩余的解题过程;
(3)淇淇在图①的基础上,将图①变为图②,其中$AB// CD,∠B= 125^{\circ },∠PQC= 65^{\circ },∠C= 145^{\circ }$,求$∠BPQ$的度数.

答案：
24.
(1) 平行于同一条直线的两条直线平行 两直线平行，同旁内角互补
(2)
∵ $\angle B = 125^{\circ}$，
∴ $\angle BPQ = 55^{\circ}$。
∵ $\angle CPQ = 25^{\circ}$，
∴ $\angle BPC = \angle BPQ + \angle CPQ = 55^{\circ} + 25^{\circ} = 80^{\circ}$。
(3) 如答图，过点 $Q$ 作 $QF // AB$，过点 $P$ 作 $PE // AB$，则 $PE // QF$。
∵ $AB // CD$，
∴ $QF // CD$。
∴ $\angle C + \angle CQF = 180^{\circ}$。
∵ $\angle C = 145^{\circ}$，
∴ $\angle CQF = 35^{\circ}$。
∵ $\angle PQC = 65^{\circ}$，
∴ $\angle PQF = 30^{\circ}$。
∵ $PE // QF$，
∴ $\angle EPQ = \angle PQF = 30^{\circ}$。
∵ $AB // PE$，$\angle B = 125^{\circ}$，
∴ $\angle BPE = 180^{\circ} - \angle B = 55^{\circ}$。
∴ $\angle BPQ = \angle BPE + \angle EPQ = 85^{\circ}$。

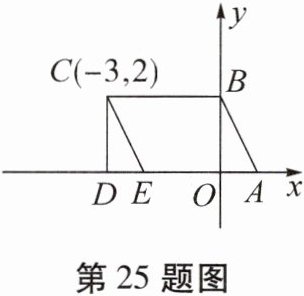
25. 如图,点$A(1,0)$,点B在y轴上,将三角形OAB沿x轴负半轴平移,平移后的图形是三角形DEC,点C的坐标是$(-3,2).$
(1)点B的坐标是(0, 2),点E的坐标是(-2, 0).
(2)点P从点O出发,沿$OB→BC→CD$移动,若点P的速度是每秒1个单位长度,运动时间是$ts(t＞0).$
①用含t的式子表示点P的坐标.
②当t的值是多少时,点P的横坐标与纵坐标互为相反数?
③当三角形AEP的面积是2时,直接写出此时t的值.

答案： 25.
(1) $(0, 2)$ $(-2, 0)$
(2) ① 当点 $P$ 在 $OB$ 上时，点 $P$ 的坐标为 $(0, t)$。当点 $P$ 在 $BC$ 上时，点 $P$ 的横坐标为 $-(t - 2) = 2 - t$，纵坐标为 2，
∴ 点 $P$ 的坐标为 $(2 - t, 2)$。当点 $P$ 在 $CD$ 上时，点 $P$ 的横坐标为 $-3$，纵坐标为 $2 + 3 + 2 - t = 7 - t$。
∴ 点 $P$ 的坐标为 $(-3, 7 - t)$。②
∵ 点 $P$ 的横坐标与纵坐标互为相反数，$t ＞ 0$，
∴ 点 $P$ 在 $BC$ 上。
∴ $2 - t + 2 = 0$。解得 $t = 4$。
∴ 当 $t = 4$ 时，点 $P$ 的横坐标与纵坐标互为相反数。③ $t = \dfrac{4}{3}$ 或 $t = \dfrac{17}{3}$。