《2025年暑期升级训练七年级数学浙教版浙江教育出版社》

1.(西藏中考)随着我国科技迅猛发展,电子制造技术不断取得突破性成就,电子元件尺寸越来越小,在芯片上某种电子元件大约占$0.0000007mm^{2}$,将0.0000007用科学记数法表示应为()

A.$0.7×10^{-7}$
B.$0.7×10^{-6}$
C.$7×10^{-7}$
D.$7×10^{-6}$

答案： C

2.(菏泽中考)下列运算正确的是()

A.$a^{6}÷a^{3}= a^{2}$
B.$a^{2}\cdot a^{3}= a^{5}$
C.$(2a^{3})^{2}= 2a^{6}$
D.$(a+b)^{2}= a^{2}+b^{2}$

答案： B

3. 若$a= -3^{-2},b= (-\frac {1}{3})^{-2},c= (-0.3)^{0}$,则a,b,c的大小关系是()

A.$a\lt b\lt c$
B.$b\lt c\lt a$
C.$c\lt b\lt a$
D.$a\lt c\lt b$

答案： D

4. 有下列计算：①$(x+2y)(x-2y)= x^{2}-2y^{2}$；②$(-x+y)^{2}= x^{2}-2xy+y^{2}$；③$(-a+b)\cdot (a-b)= a^{2}-b^{2}$；④$(-2a-3)(2a-3)= 9-4a^{2}$；⑤$(a-b)^{2}= a^{2}-b^{2}$。其中,正确的有()

A.4个
B.3个
C.2个
D.1个

答案： C
方法点金
运用乘法公式时的注意点
运用乘法公式时应注意以下几点:
(1) 平方差公式和完全平方公式中的 $ a $, $ b $ 可以是单项式, 也可以是多项式.
(2) 弄清公式中的结构形式, 是正确运用乘法公式的关键所在.
(3) 运用平方差公式计算时, 关键要找相同项和相反项, 其结果是相同项的平方减去相反项的平方; 运用完全平方公式计算时, 应注意展开后的结构特征是“首平方, 末平方, 首末两倍中间放”, 特别要注意中间项的符号.

5. 数学课上,老师讲了单项式乘多项式。放学回到家后,明明拿出课堂笔记复习,发现一道题：$-3xy\cdot (4y-2x-1)= -12xy^{2}+6x^{2}y□$。其中“□”表示被墨水弄污的部分,这个部分为()

A.$+3xy$
B.$-3xy$
C.$-1$
D.$+1$

答案： A

6. 整体思想 已知$(x+2)(x-2)-2x= 1$,则$2x^{2}-4x+3$的值为()

A.13
B.8
C.$-3$
D.5

答案： A

7. 已知$4^{m}= a,8^{n}= b$,其中m,n为正整数,则$2^{2m+6n}$等于()

A.$ab^{2}$
B.$a+b^{2}$
C.$a^{2}b^{3}$
D.$a^{2}+b^{3}$

答案： A

8. 若$x+m与x+3$的乘积中不含x的一次项,则m的值为()

A.0
B.3
C.$-1$
D.$-3$

答案： D

9. 如图,在边长为$m+n$的正方形纸片中剪去一个边长为m的小正方形纸片之后,剩余部分又剪拼成一个长方形(不重叠、无缝隙)。若拼成的长方形的一边长为n,则与其相邻的另一边长为()


A.$m+2n$
B.$2m+n$
C.$m+n$
D.$2(m+n)$

答案： B

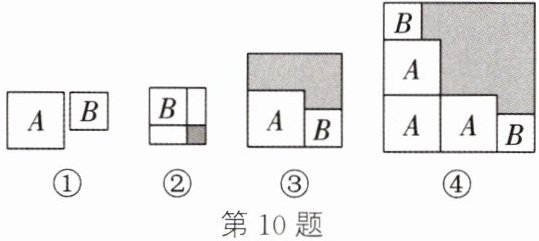
10. 如图①,有两张正方形纸片A,B。将B放在A的内部得到图②。如图③,将A,B并列摆放后,构造出一个新的正方形。若图②和图③中涂色部分的面积分别为1和12,现将三张正方形纸片A和两张正方形纸片B按如图④所示的方式摆放,则图④中涂色部分的面积为()


A.28
B.29
C.30
D.31

答案： B 解析: 设正方形纸片 $ A $, $ B $ 的边长分别为 $ a $, $ b ( a ＞ b ) $. 由题图②中涂色部分的面积为 1, 可得 $ ( a - b ) ^ { 2 } = 1 $, 所以 $ a - b = 1 $. 由题图③中涂色部分的面积为 12, 可得 $ ( a + b ) ^ { 2 } - ( a ^ { 2 } + b ^ { 2 } ) = 2 a b = 12 $. 所以 $ ( a + b ) ^ { 2 } = ( a - b ) ^ { 2 } + 4 a b = 1 + 2 × 12 = 25 $. 所以 $ a + b = 5 $. 所以题图④中涂色部分的面积为 $ ( 2 a + b ) ^ { 2 } - ( 3 a ^ { 2 } + 2 b ^ { 2 } ) = a ^ { 2 } + 4 a b - b ^ { 2 } = ( a + b ) ( a - b ) + 4 a b = 5 × 1 + 2 × 12 = 29 $.
方法点金
运用乘法公式的常见变形解题
运用平方差公式和完全平方公式进行计算时, 注意运用它们的变形形式. 完全平方公式的常见变形: ① $ a ^ { 2 } + b ^ { 2 } = ( a + b ) ^ { 2 } - 2 a b = ( a - b ) ^ { 2 } + 2 a b $; ② $ ( a + b ) ^ { 2 } + ( a - b ) ^ { 2 } = 2 a ^ { 2 } + 2 b ^ { 2 } $; ③ $ a b = \frac { 1 } { 2 } [ ( a + b ) ^ { 2 } - ( a ^ { 2 } + b ^ { 2 } ) ] = \frac { 1 } { 4 } [ ( a + b ) ^ { 2 } - ( a - b ) ^ { 2 } ] $. 平方差公式的常见变形: ① $ ( a + b ) ( - a + b ) = b ^ { 2 } - a ^ { 2 } $; ② $ ( - a - b ) \cdot ( a - b ) = b ^ { 2 } - a ^ { 2 } $; ③ $ ( a + 2 b - c ) ( a - 2 b + c ) = a ^ { 2 } - ( 2 b - c ) ^ { 2 } $; ④ $ ( a + b ) ( a - b ) ( a ^ { 2 } + b ^ { 2 } ) = a ^ { 4 } - b ^ { 4 } $.

11. 计算：$(\frac {1}{7})^{2025}×(-7)^{2025}+7^{0}= $____。

答案： 0