《2025年暑期升级训练七年级数学浙教版浙江教育出版社》

12. 小明在计算$(8a^{3}b-M)÷4ab$时,把括号内M前的减号不小心看成了乘号,最后计算的错误结果是$10a^{4}b$,那么正确的结果是____。

答案： $ 2 a ^ { 2 } - \frac { 5 } { 4 } a $

13. 已知$(x+y)^{2}= 25,(x-y)^{2}= 9$,则$xy= $____。

答案： 4

14. 整体思想 若$(m+58)^{2}= 654483$,则$(m+48)(m+68)$的值为____。

答案： 654 383

15. 数形结合思想 小聪在学习完乘法公式后,发现完全平方公式经过适当变形或数形结合,可以解决很多数学问题。两张正方形卡片按如图所示的方式放置,点A,M,B在同一条直线上。若$AB= 10$,两正方形的面积之和为52,则涂色部分的面积是____。

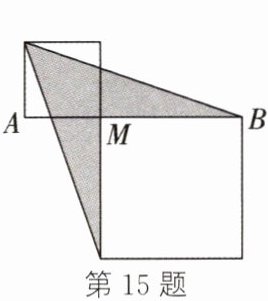
答案： 24 解析: 设小正方形的边长为 $ a $, 大正方形的边长为 $ b $. 因为 $ A B = 10 $, 两正方形的面积之和为 52, 所以 $ a + b = 10 $, $ a ^ { 2 } + b ^ { 2 } = 52 $, 则涂色部分的面积 $ = ( a + b ) ^ { 2 } - 2 × \frac { 1 } { 2 } a ( a + b ) - b ^ { 2 } = a ^ { 2 } + b ^ { 2 } + 2 a b - a ^ { 2 } - a b - b ^ { 2 } = a b = \frac { ( a + b ) ^ { 2 } - ( a ^ { 2 } + b ^ { 2 } ) } { 2 } = \frac { 100 - 52 } { 2 } = 24 $.

16. 四张长为a、宽为$b(a＞b)的长方形纸片和一张边长为a-b的正方形纸片按如图所示的方式拼成一个边长为a+b$的正方形,图中空白部分的面积为$S_{1}$,涂色部分的面积为$S_{2}$。若$S_{1}= S_{2}$,则$a:b= $____。

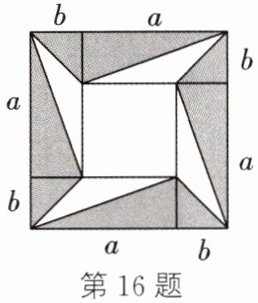
答案： $ 3 : 1 $ 解析: 由题意, 得 $ S _ { 2 } = 4 \left( \frac { 1 } { 2 } a b + \frac { 1 } { 2 } b ^ { 2 } \right) = 2 a b + 2 b ^ { 2 } $, $ S _ { 1 } = ( a + b ) ^ { 2 } - S _ { 2 } = a ^ { 2 } + 2 a b + b ^ { 2 } - 2 a b - 2 b ^ { 2 } = a ^ { 2 } - b ^ { 2 } $. 根据 $ S _ { 1 } = S _ { 2 } $ 可知, $ a ^ { 2 } - b ^ { 2 } = 2 a b + 2 b ^ { 2 } $, 从而得到 $ a ^ { 2 } - 2 a b = 3 b ^ { 2 } $. 在等号两边同时加上 $ b ^ { 2 } $, 得到 $ ( a - b ) ^ { 2 } = 4 b ^ { 2 } $, 从而可得 $ a - b = 2 b $ 或 $ a - b = - 2 b $ (不合题意, 舍去). 所以 $ a = 3 b $. 所以 $ a : b = 3 : 1 $.

17.(9分)计算：
(1)$(-\frac {1}{4})^{-1}+(-2)^{2}×2023^{0}-(\frac {1}{3})^{-2}$。
(2)$(-3bx^{2})^{3}\cdot b^{3}÷(9b^{2}x)$。
(3)(陕西中考)$(x-1)(x+2)-3(x-1)$。

答案：
(1) -9.
(2) $ - 3 b ^ { 4 } x ^ { 5 } $.
(3) $ x ^ { 2 } - 2 x + 1 $.

18.(8分)先化简,再求值：
(1)(甘肃中考)$[(2a+b)^{2}-(2a+b)(2a-b)]÷(2b)$,其中$a= 2,b= -1$。
(2)(西宁中考)$(3a-1)^{2}-2a(4a-1)$,其中a满足$a^{2}-4a+3= 0$。

答案：
(1) 原式 $ = [ 4 a ^ { 2 } + 4 a b + b ^ { 2 } - ( 4 a ^ { 2 } - b ^ { 2 } ) ] ÷ ( 2 b ) = ( 4 a ^ { 2 } + 4 a b + b ^ { 2 } - 4 a ^ { 2 } + b ^ { 2 } ) ÷ ( 2 b ) = ( 4 a b + 2 b ^ { 2 } ) ÷ ( 2 b ) = 2 a + b $. 当 $ a = 2 $, $ b = - 1 $ 时, 原式 $ = 2 × 2 - 1 = 3 $.
(2) 原式 $ = ( 9 a ^ { 2 } - 6 a + 1 ) - 8 a ^ { 2 } + 2 a = ( 9 a ^ { 2 } - 8 a ^ { 2 } ) + ( - 6 a + 2 a ) + 1 = a ^ { 2 } - 4 a + 1 $. 因为 $ a ^ { 2 } - 4 a + 3 = 0 $, 所以 $ a ^ { 2 } - 4 a = - 3 $. 所以原式 $ = - 3 + 1 = - 2 $.