第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
22.(8 分)某校欲购置规格分别为 300mL 和 500mL 的甲、乙两种免洗手消毒液若干瓶。已知购买 1 瓶甲种免洗手消毒液和 1 瓶乙种免洗手消毒液需要 32 元,购买 5 瓶甲种免洗手消毒液和 3 瓶乙种免洗手消毒液需要 120 元。
(1)求甲、乙两种免洗手消毒液的单价。
(2)该校在校师生共 1000 人,平均每人每天需使用 10mL 的免洗手消毒液。若校方购买甲、乙两种免洗手消毒液共花费 4000 元,则这批免洗手消毒液可使用多少天?
(3)为节约成本,该校购买散装免洗手消毒液进行分装,现需将 9.6L 的免洗手消毒液全部装入最大容量分别为 300mL 和 500mL 的两种空瓶中(每瓶均装满)。若分装时平均每瓶损耗 20mL,则如何分装能使总损耗最小?求出此时需要两种空瓶各多少个(每种至少需要 1 个)。
(1)求甲、乙两种免洗手消毒液的单价。
(2)该校在校师生共 1000 人,平均每人每天需使用 10mL 的免洗手消毒液。若校方购买甲、乙两种免洗手消毒液共花费 4000 元,则这批免洗手消毒液可使用多少天?
(3)为节约成本,该校购买散装免洗手消毒液进行分装,现需将 9.6L 的免洗手消毒液全部装入最大容量分别为 300mL 和 500mL 的两种空瓶中(每瓶均装满)。若分装时平均每瓶损耗 20mL,则如何分装能使总损耗最小?求出此时需要两种空瓶各多少个(每种至少需要 1 个)。
答案:
(1) 设甲种免洗手消毒液的单价为 x 元,乙种免洗手消毒液的单价为 y 元. 由题意,得 $\begin{cases} x + y = 32, \\ 5x + 3y = 120, \end{cases}$ 解得 $\begin{cases} x = 12, \\ y = 20. \end{cases}$ 所以甲种免洗手消毒液的单价为 12 元,乙种免洗手消毒液的单价为 20 元.
(2) 设购买甲种免洗手消毒液 a 瓶,乙种免洗手消毒液 b 瓶. 由题意,得 12a + 20b = 4000. 化简,得 3a + 5b = 1000. 所以 $\frac{300a + 500b}{1000×10}$ = $\frac{100(3a + 5b)}{1000×10}$ = $\frac{100×1000}{1000×10}$ = 10(天). 所以这批免洗手消毒液可使用 10 天.
(3) 9.6 L = 9600 mL. 设需要 300 mL 的空瓶 m 个,500 mL 的空瓶 n 个. 由题意,得 300m + 500n + 20(m + n) = 9600. 化简,得 m = 30 - $\frac{13}{8}$n. 因为 m,n 均为正整数,所以 $\begin{cases} m = 17, \\ n = 8 \end{cases}$ 或 $\begin{cases} m = 4, \\ n = 16. \end{cases}$ 因为要使分装时总损耗最小,即 20(m + n) 最小,所以 $\begin{cases} m = 4, \\ n = 16. \end{cases}$ 所以分装时需要 300 mL 的空瓶 4 个,500 mL 的空瓶 16 个.
(1) 设甲种免洗手消毒液的单价为 x 元,乙种免洗手消毒液的单价为 y 元. 由题意,得 $\begin{cases} x + y = 32, \\ 5x + 3y = 120, \end{cases}$ 解得 $\begin{cases} x = 12, \\ y = 20. \end{cases}$ 所以甲种免洗手消毒液的单价为 12 元,乙种免洗手消毒液的单价为 20 元.
(2) 设购买甲种免洗手消毒液 a 瓶,乙种免洗手消毒液 b 瓶. 由题意,得 12a + 20b = 4000. 化简,得 3a + 5b = 1000. 所以 $\frac{300a + 500b}{1000×10}$ = $\frac{100(3a + 5b)}{1000×10}$ = $\frac{100×1000}{1000×10}$ = 10(天). 所以这批免洗手消毒液可使用 10 天.
(3) 9.6 L = 9600 mL. 设需要 300 mL 的空瓶 m 个,500 mL 的空瓶 n 个. 由题意,得 300m + 500n + 20(m + n) = 9600. 化简,得 m = 30 - $\frac{13}{8}$n. 因为 m,n 均为正整数,所以 $\begin{cases} m = 17, \\ n = 8 \end{cases}$ 或 $\begin{cases} m = 4, \\ n = 16. \end{cases}$ 因为要使分装时总损耗最小,即 20(m + n) 最小,所以 $\begin{cases} m = 4, \\ n = 16. \end{cases}$ 所以分装时需要 300 mL 的空瓶 4 个,500 mL 的空瓶 16 个.
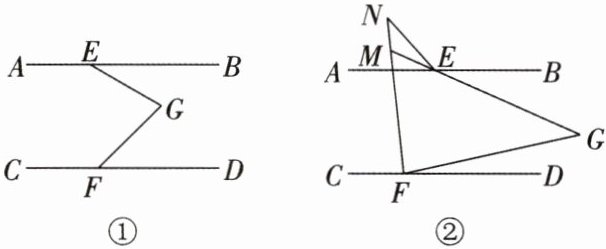
23.(10 分)已知直线$AB// CD$,点 E 在直线 AB 上,点 F 在直线 CD 上,G 是平面内一点。
(1)如图①,点 G 在直线 AB,CD 之间,若$∠BEG = 30^{\circ}$,$∠EGF = 75^{\circ}$,求$∠DFG$的度数。
(2)如图②,点 G 在直线 AB,CD 之间。FN 平分$∠CFG$,延长 GE 交 FN 于点 M,EM 平分$∠AEN$。当$∠N+\frac{1}{2}∠FGE = 54^{\circ}$时,求$∠AEN$的度数。
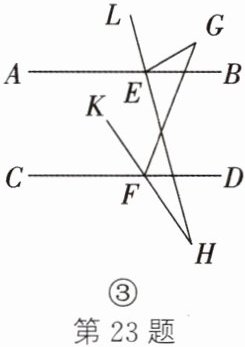
(3)如图③,点 G 在直线 AB 上方,FK 平分$∠CFG$,EL 平分$∠AEG$,直线 KF 与直线 LE 相交于点 H,试猜想$∠EGF与∠EHF$之间的数量关系,并说明理由。
(1)如图①,点 G 在直线 AB,CD 之间,若$∠BEG = 30^{\circ}$,$∠EGF = 75^{\circ}$,求$∠DFG$的度数。
(2)如图②,点 G 在直线 AB,CD 之间。FN 平分$∠CFG$,延长 GE 交 FN 于点 M,EM 平分$∠AEN$。当$∠N+\frac{1}{2}∠FGE = 54^{\circ}$时,求$∠AEN$的度数。
(3)如图③,点 G 在直线 AB 上方,FK 平分$∠CFG$,EL 平分$∠AEG$,直线 KF 与直线 LE 相交于点 H,试猜想$∠EGF与∠EHF$之间的数量关系,并说明理由。


答案:
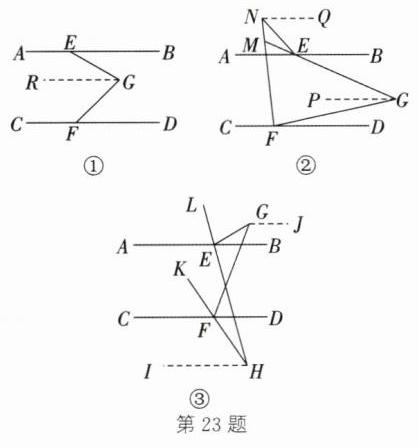
(1) 如图①,过点 G 作 GR//AB. 因为 AB//CD,所以 AB//CD//GR. 所以 ∠BEG = ∠EGR,∠DFG = ∠FGR. 所以 ∠BEG + ∠DFG = ∠EGR + ∠FGR = ∠EGF. 因为 ∠BEG = 30°,∠EGF = 75°,所以 ∠DFG = 45°.
(2) 因为 FN 平分 ∠CFG,EM 平分 ∠AEN,所以可设 ∠CFN = ∠GFN = β,∠AEM = ∠NEM = α. 如图②,过点 G 作 GP//CD,过点 N 作 NQ//AB. 又因为 AB//CD,所以 NQ//AB//CD//GP. 所以 ∠QNF = ∠CFN = β,∠QNE = ∠AEN = 2α,∠PGE = ∠AEM = α,∠PGF = ∠DFG = 180° - 2β. 所以 ∠FNE = ∠QNF - ∠QNE = β - 2α,∠FGE = ∠PGE + ∠PGF = α + 180° - 2β. 又因为 ∠FNE + $\frac{1}{2}$∠FGE = 54°,所以 β - 2α + $\frac{1}{2}$(α + 180° - 2β) = 54°, 解得 α = 24°. 所以 ∠AEN = 2α = 48°.
(3) ∠EGF = 2∠EHF. 理由:因为 FK 平分 ∠CFG,EL 平分 ∠AEG,所以可设 ∠CFK = ∠GFK = n,∠AEL = ∠LEG = m. 如图③,过点 H 作 HI//CD,过点 G 作 GJ//AB. 因为 AB//CD,所以 GJ//AB//CD//HI. 所以 ∠JGE = ∠AEG = 2m,∠JGF = ∠CFG = 2n,∠IHK = ∠CFK = n,∠IHL = ∠AEL = m. 所以 ∠EGF = ∠JGE - ∠JGF = 2m - 2n = 2(m - n),∠EHF = ∠IHL - ∠IHK = m - n. 所以 ∠EGF = 2∠EHF.
(1) 如图①,过点 G 作 GR//AB. 因为 AB//CD,所以 AB//CD//GR. 所以 ∠BEG = ∠EGR,∠DFG = ∠FGR. 所以 ∠BEG + ∠DFG = ∠EGR + ∠FGR = ∠EGF. 因为 ∠BEG = 30°,∠EGF = 75°,所以 ∠DFG = 45°.
(2) 因为 FN 平分 ∠CFG,EM 平分 ∠AEN,所以可设 ∠CFN = ∠GFN = β,∠AEM = ∠NEM = α. 如图②,过点 G 作 GP//CD,过点 N 作 NQ//AB. 又因为 AB//CD,所以 NQ//AB//CD//GP. 所以 ∠QNF = ∠CFN = β,∠QNE = ∠AEN = 2α,∠PGE = ∠AEM = α,∠PGF = ∠DFG = 180° - 2β. 所以 ∠FNE = ∠QNF - ∠QNE = β - 2α,∠FGE = ∠PGE + ∠PGF = α + 180° - 2β. 又因为 ∠FNE + $\frac{1}{2}$∠FGE = 54°,所以 β - 2α + $\frac{1}{2}$(α + 180° - 2β) = 54°, 解得 α = 24°. 所以 ∠AEN = 2α = 48°.
(3) ∠EGF = 2∠EHF. 理由:因为 FK 平分 ∠CFG,EL 平分 ∠AEG,所以可设 ∠CFK = ∠GFK = n,∠AEL = ∠LEG = m. 如图③,过点 H 作 HI//CD,过点 G 作 GJ//AB. 因为 AB//CD,所以 GJ//AB//CD//HI. 所以 ∠JGE = ∠AEG = 2m,∠JGF = ∠CFG = 2n,∠IHK = ∠CFK = n,∠IHL = ∠AEL = m. 所以 ∠EGF = ∠JGE - ∠JGF = 2m - 2n = 2(m - n),∠EHF = ∠IHL - ∠IHK = m - n. 所以 ∠EGF = 2∠EHF.

查看更多完整答案,请扫码查看


