《2025年暑期升级训练七年级数学浙教版浙江教育出版社》

1. 下列各式由左到右的变形中,属于因式分解的是()

A.$(x+2)(x-2)= x^{2}-4$
B.$x^{2}-4= (x+2)(x-2)$
C.$x^{2}-4+3x= (x+2)(x-2)+3x$
D.$x^{2}+4x-2= x(x+4)-2$

答案： B

2. 多项式$8a^{3}b^{2}+12ab^{3}c$的公因式为()

A.$abc$
B.$4ab^{2}$
C.$ab^{2}$
D.$4ab^{2}c$

答案： B

3. 小明在抄分解因式的题目时,不小心漏抄了$x$的指数,他只知道该指数为不大于10的正整数,并且能利用平方差公式分解因式,他抄在作业本上的式子为$x^{□}-4y^{2}$(“□”表示漏抄的指数),则这个指数可能的结果共有()

A.2种
B.3种
C.4种
D.5种

答案： D

4. 计算$125^{2}-50×125+25^{2}$的结果是()

A.100
B.150
C.10000
D.22500

答案： C

5. 已知$xy= 3,x-y= -2$,则代数式$x^{2}y-xy^{2}$的值是()

A.6
B.-1
C.-5
D.-6

答案： D

6. 新情境 游戏活动 琪琪是一名密码翻译爱好者,在她的密码手册中,有这样一条信息：$a-b,x-y,x+y,a+b,x^{2}-y^{2},a^{2}-b^{2}$分别对应下列六个字：华、爱、我、中、丽、美.现将$(x^{2}-y^{2})a^{2}-(x^{2}-y^{2})b^{2}$分解因式,结果呈现的密码信息可能是()

A.我爱美
B.中华美丽
C.我爱中华
D.美我中华

答案： C

7. (河北中考)若$k$为任意整数,则$(2k+3)^{2}-4k^{2}$的值总能()

A.被2整除
B.被3整除
C.被5整除
D.被7整除

答案： B

8. 如图,有一张边长为$b$的正方形纸板,先在它的四角各剪去一个边长为$a$的正方形,然后将四周突出的部分折起,制成一个无盖的长方体纸盒.用$M$表示其底面积与侧面积的差,则$M$可分解因式为()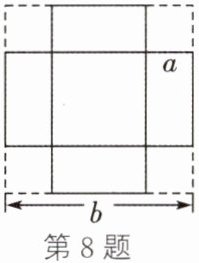

A.$(b-6a)(b-2a)$
B.$(b-3a)(b-2a)$
C.$(b-5a)(b-a)$
D.$(b-2a)^{2}$

答案： 8. A 解析：由题意，得这个长方体纸盒的底面积为$(b - 2a)^{2}$，侧面积为$4a(b - 2a)$，所以$M = (b - 2a)^{2} - 4a(b - 2a)$。提取公因式$b - 2a$，即可得到$M = (b - 2a)(b - 2a - 4a) = (b - 2a)(b - 6a)$。

9. 已知$a^{2}(b+c)= b^{2}(a+c)= 2025$,且$a,b,c$互不相等,则$abc$的值为()

A.2025
B.-2025
C.1
D.-1

答案： 9. B 解析：因为$a^{2}(b + c) = b^{2}(a + c)$，所以$a^{2}b + a^{2}c - ab^{2} - b^{2}c = 0$。所以$ab(a - b) + c(a + b)(a - b) = 0$。所以$(a - b)(ab + ac + bc) = 0$。由$a \neq b$可知，$ab + ac + bc = 0$。所以$ab + ac = - bc$。由$a^{2}(b + c) = 2025$，可得$a(ab + ac) = 2025$。所以$a(- bc) = 2025$，即$abc = - 2025$。
方法点金
运用分组分解法分解因式
分组分解法一般是针对四项或四项以上多项式的因式分解，分组有两个目的，一是分组后能出现公因式，二是分组后能运用公式。
对于常见的四项式，一般的分组分解法有两种形式：①二二分法；②三一分法。例如：$ax + ay + bx + by = x(a + b) + y(a + b) = (a + b)(x + y)$；$2xy - x^{2} + 1 - y^{2} = - (x^{2} - 2xy + y^{2}) + 1 = 1 - (x - y)^{2} = (1 + x - y)(1 - x + y)$。

10. 已知三个实数$a,b,c满足a-2b+c= 0,a+2b+c＜0$,则下列结论中,正确的是()

A.$b＞0,b^{2}-ac≤0$
B.$b＜0,b^{2}-ac≤0$
C.$b＞0,b^{2}-ac≥0$
D.$b＜0,b^{2}-ac≥0$

答案： 10. D 解析：因为$a - 2b + c = 0$，$a + 2b + c \lt 0$。所以$a + c = 2b$，$b = \frac{a + c}{2}$。所以$a + 2b + c = (a + c) + 2b = 4b \lt 0$。所以$b \lt 0$。所以$b^{2} - ac = (\frac{a + c}{2})^{2} - ac = \frac{a^{2} + 2ac + c^{2}}{4} - ac = \frac{a^{2} - 2ac + c^{2}}{4} = (\frac{a - c}{2})^{2} \geq 0$。

11. 分解因式：$25x^{2}-16y^{2}= $.

答案： $(5x + 4y)(5x - 4y)$

12. 将多项式$3m^{2}n^{3}-12m^{2}n$分解因式时,应提取的公因式为,该多项式进行因式分解的最后结果为.

答案： $3m^{2}n$ $3m^{2}n(n - 2)(n + 2)$

13. 运用因式分解把9991分解成两个自然数的积,则这两个自然数为.

答案： 103.97

14. 甲、乙两名同学将一个二次三项式因式分解,甲同学因看错了一次项系数而分解成$2(x-1)(x-9)$；乙同学因看错了常数项而分解成$2(x-2)(x-4)$.原二次三项式为,因式分解的正确结果为.

答案： $2x^{2} - 12x + 18$ $2(x - 3)^{2}$