《2025年暑期升级训练七年级数学浙教版浙江教育出版社》

6. 我们面对没有学过的数学题时,方法可以创新,但在创新中要遵循法则和运算律,才能正确解答. 下面介绍一种分解因式的新方法—拆项补项法：把多项式的某一项拆开或填补上互为相反数的两项(或几项),使原式转化为已学过的知识进行分解.
例题：用拆项补项法分解因式：$ x^{3}-9 x+8 $.
解：原式 $ =x^{3}-x^{2}+x^{2}-9 x+8 $
$ =x^{3}-x^{2}+x^{2}-x-8 x+8 $
$ =x^{2}(x-1)+x(x-1)-8(x-1) $
$ =(x-1)\left(x^{2}+x-8\right) $.
请你结合自己的思考和理解分解因式：
(1)$ x^{3}+9 x-10 $.
(2)$ x^{3}-2 x^{2}-5 x+6 $.

答案：
(1)原式$=x^{3}-x^{2}+x^{2}+9x-10=x^{2}(x-1)+(x-1)(x+10)=(x-1)(x^{2}+x+10)$.
(2)原式$=x^{3}-3x^{2}+x^{2}-5x+6=x^{2}(x-3)+(x-2)(x-3)=(x-3)(x^{2}+x-2)=(x-3)(x+2)(x-1)$.

7. 如图甲,将一张长方形纸板按图中虚线裁剪成 9 块,若图中①②都是边长为 $ a $ 的大正方形,③④都是边长为 $ b $ 的小正方形,剩下的都是边长分别为 $ a $,$ b $ 的小长方形.

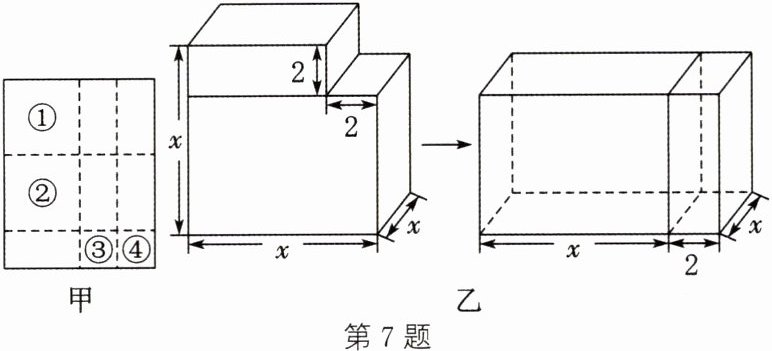
(1)观察图甲,可以发现多项式 $ 2 a^{2}+5 a b+2 b^{2} $ 因式分解为______.
(2)若图甲中每个小长方形的面积为 4,四个正方形的面积之和为 34,试求图甲中所有裁剪线(虚线部分)长之和.
(3)如图乙所示的为一个棱长是 $ x $ 的正方体切去一个小长方体后重新拼成一个新长方体,请你根据图形的体积变化关系,直接写出一个因式分解形式的等式.

答案：
(1)$(2a+b)(a+2b)$.
(2)由题意,得$ab=4,2a^{2}+2b^{2}=34$,所以$a^{2}+b^{2}=17$.所以$(a+b)^{2}=a^{2}+b^{2}+2ab=25$.因为$a＞0,b＞0$,所以$a+b=5$.所以所有裁剪线(虚线部分)长之和为$2(2a+b)+2(a+2b)=6a+6b=6×5=30$.
(3)因为拼接过程中新长方体的体积不变,所以$x^{3}-4x=x(x+2)(x-2)$.