《2025年暑期升级训练七年级数学浙教版浙江教育出版社》

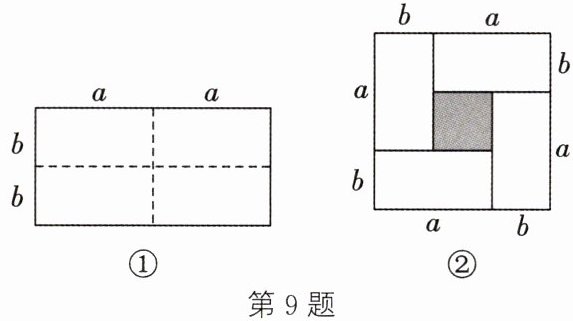
9. 如图①所示为一个长为$2a$、宽为$2b$的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.
答案讲解
(1) 请观察图①和图②的面积关系,直接写出代数式$(a+b)^{2},(a-b)^{2},ab$之间的等量关系:____.
(2) 根据(1)中的等量关系,解决如下问题:
① 已知$m+n= 5,mn= -14$,求$(m-n)^{2}$的值.
② 已知$x＞0,x-\frac{2}{x}= 1$,求$x+\frac{2}{x}$的值.

答案：
(1) $ 4ab=(a + b)^{2}-(a - b)^{2} $。
(2) ① $ (m - n)^{2}=(m + n)^{2}-4mn=25 + 56 = 81 $。② 因为 $ (x+\frac{2}{x})^{2}=(x-\frac{2}{x})^{2}+8 = 1 + 8 = 9 $，而 $ x ＞ 0 $，所以 $ x+\frac{2}{x}=3 $。

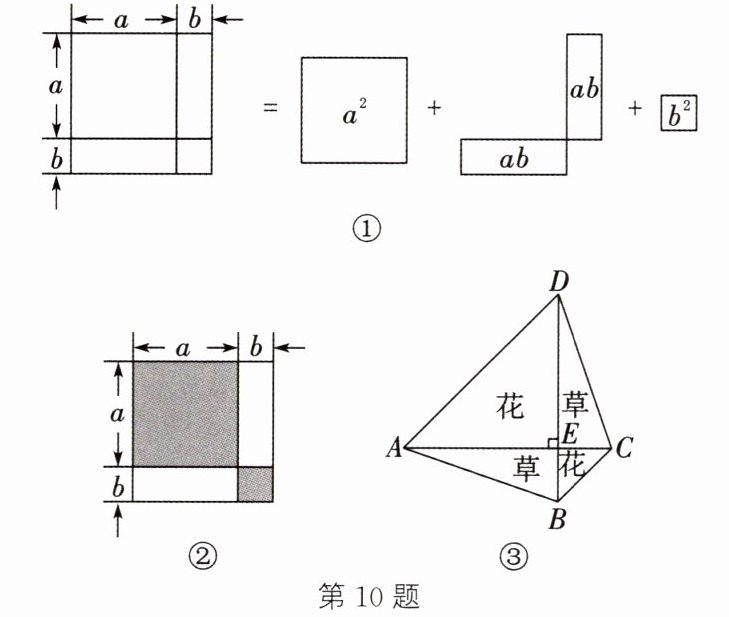
10. 用等式表示图①中图形的面积为$(a+b)^{2}= a^{2}+2ab+b^{2}$.
答案讲解
(1) 用等式表示图②中涂色部分的面积和为____.
(2) 根据图②所得的公式,若$a+b= 15,ab= 4$,则$a^{2}+b^{2}= $____.
(3) 若$x满足(5-x)(x-1)= 2$,求$(5-x)^{2}+(x-1)^{2}$的值.
(4) 如图③,某学校有一块梯形空地$ABCD,AC⊥BD于点E,AE= DE,BE= CE$. 该校计划在三角形$AED和三角形BEC$区域内种花,在三角形$CDE和三角形ABE$区域内种草. 经测量,种花区域的面积和为 109 平方米,$AC= 18$米,求种草区域的面积和.

答案：
(1) $ a^{2}+b^{2}=(a + b)^{2}-2ab $。
(2) 217。
(3) 设 $ m = 5 - x $，$ n = x - 1 $，则 $ m + n = 4 $，$ mn=(5 - x)(x - 1)=2 $。所以 $ (5 - x)^{2}+(x - 1)^{2}=m^{2}+n^{2}=(m + n)^{2}-2mn=16 - 4 = 12 $。
(4) 设 $ AE = DE = a $ 米，$ BE = CE = b $ 米。由题意，得 $ a + b = 18 $，$ S_{三角形AED}+S_{三角形BEC}=\frac{1}{2}a^{2}+\frac{1}{2}b^{2}=109 $（平方米），即 $ a^{2}+b^{2}=218 $，所以 $ S_{三角形CDE}+S_{三角形ABE}=\frac{1}{2}ab+\frac{1}{2}ab=ab=\frac{(a + b)^{2}-(a^{2}+b^{2})}{2}=\frac{324 - 218}{2}=53 $（平方米），即种草区域的面积和为 53 平方米。