《2025年暑期升级训练七年级数学浙教版浙江教育出版社》

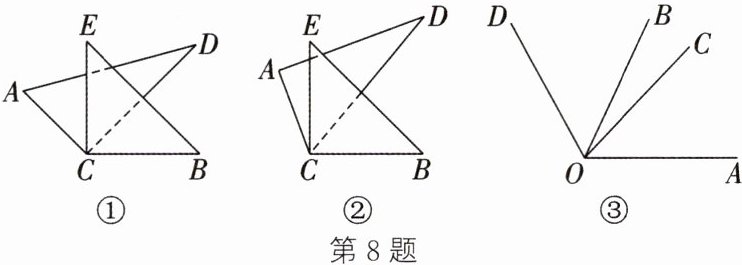
8. 用一副三角尺(一把含$45^{\circ}$角,一把含$30^{\circ}$角)来探究两个角之间的关系。
(1) 如图①,将两把三角尺的直角顶点C叠放在一起,使CD落在$∠BCE$的内部。
① 若CD平分$∠BCE$,则$∠DCE$的度数为______$^{\circ}$,$∠ACB$的度数为______$^{\circ}$。
② 猜想$∠ACB与∠DCE$的大小有何关系,并说明理由。
(2) 如图②,将含$45^{\circ}角的三角尺的直角顶点与含60^{\circ}角的三角尺的60^{\circ}$角的顶点重合在一起,使CD落在$∠BCE$的内部,直接写出$∠ACB + ∠DCE$的度数。
(3) 根据以上探究,有同学提出,将任意两个锐角的顶点重合,使一个角的一边落在另一个角的内部,都有类似的结论。如图③,若$∠AOB = \alpha$,$∠COD = \beta$($\alpha$,$\beta$都是锐角),它们的顶点O重合在一起,则$∠AOD与∠BOC$的大小有何关系？请说明理由。

答案：
(1) ① $ 45 $；$ 135 $。② $ \angle ACB + \angle DCE = 180^{\circ} $。理由：因为 $ \angle ACD = \angle BCE = 90^{\circ} $，所以 $ \angle DCE = 90^{\circ}-\angle BCD $。所以 $ \angle ACB + \angle DCE = \angle ACD + \angle BCD + (90^{\circ}-\angle BCD)=90^{\circ}+90^{\circ}=180^{\circ} $。
(2) 由题意，得 $ \angle BCE = 90^{\circ} $，$ \angle ACD = 60^{\circ} $，所以 $ \angle DCE = 60^{\circ}-\angle ACE $。所以 $ \angle ACB + \angle DCE = \angle BCE + \angle ACE + \angle DCE = \angle BCE + \angle ACE + (60^{\circ}-\angle ACE)=90^{\circ}+60^{\circ}=150^{\circ} $。
(3) $ \angle AOD + \angle BOC = \alpha+\beta $。理由：因为 $ \angle AOB = \alpha $，$ \angle COD = \beta $，所以 $ \angle AOC = \alpha-\angle BOC $。所以 $ \angle AOD = \angle COD + \angle AOC = \beta+\alpha-\angle BOC $。所以 $ \angle AOD + \angle BOC = \alpha+\beta $。

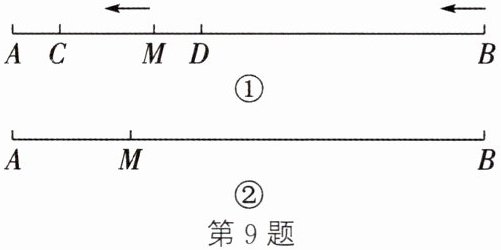
9. 如图①,M是线段AB上一点,点C在线段AM上,点D在线段BM上,C,D两点分别同时从点M,B出发,分别以1 cm/s,3 cm/s的速度沿直线BA运动,运动方向如箭头所示。
(1) 若$AB = 10$ cm,$2$ cm$ ＜ AM ＜ 4$ cm,当点C,D运动了2 s时,求$AC + MD$的长。
(2) 若点C,D运动时,总有$MD = 3AC$,求AM与AB之间的数量关系。
(3) 如图②,若$AM = \frac{1}{4}AB$,N是直线AB上一点,且$AN - BN = MN$,求$\frac{MN}{AB}$的值。

答案：

(1) 当点 $ C $，$ D $ 运动了 $ 2 s $ 时，$ CM = 2 cm $，$ BD = 6 cm $。因为 $ AB = 10 cm $，所以 $ AC + MD = AB - CM - BD = 10 - 2 - 6 = 2(cm) $。
(2) 因为 $ C $，$ D $ 两点的运动速度分别为 $ 1 cm/s $，$ 3 cm/s $，所以 $ BD = 3CM $。又因为 $ MD = 3AC $，所以 $ BD + MD = 3CM + 3AC $，即 $ BM = 3AM $。所以 $ AM = \frac{1}{4}AB $。
(3) 如图①，当点 $ N $ 在线段 $ AB $ 上时，因为 $ AN - BN = MN $，$ AN - AM = MN $，所以 $ BN = AM = \frac{1}{4}AB $。所以 $ MN = (1 - \frac{1}{4}-\frac{1}{4})AB = \frac{1}{2}AB $，即 $ \frac{MN}{AB}=\frac{1}{2} $。如图②，当点 $ N $ 在线段 $ AB $ 的延长线上时，因为 $ AN - BN = MN $，$ AN - BN = AB $，所以 $ MN = AB $，即 $ \frac{MN}{AB}=1 $。综上所述，$ \frac{MN}{AB} $ 的值为 $ \frac{1}{2} $ 或 $ 1 $。

方法点金
线段动态问题的解决方法
解决线段上的动点问题时，需要明确点的运动方向和速度，考虑点的运动会带来哪些线段长度的变化或对应位置的变化；对于一些图形位置不固定的问题，要将所有情况都一一列举出来，并利用线段的和差倍分关系进行计算。