第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
1. 全等图形:能够____的两个图形称为全等图形。
答案:
1. 重合
2. 全等三角形:能够____的两个三角形叫作全等三角形。两个全等三角形重合时,能互相重合的顶点叫作全等三角形的____,互相重合的边叫作全等三角形的____,互相重合的角叫作全等三角形的____。
答案:
2. 重合 对应顶点 对应边 对应角
3. 全等三角形的性质:全等三角形的对应边____,对应角____。
答案:
3. 相等 相等
典例1
下列四个选项中,属于全等图形的是()
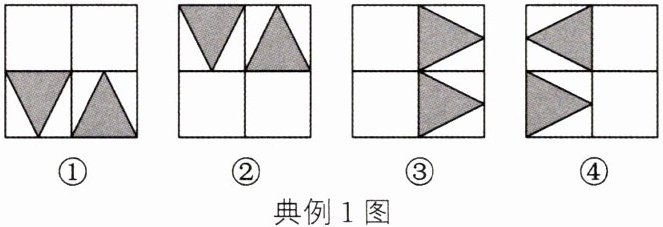
点拨 根据全等图形的概念,能够完全重合的两个图形是全等图形可得答案。
解答:
解有所悟:一个图形经过平移、翻折、旋转后得到的新图形与原图形是全等图形。
A.①和②
B.②和③
C.①和③
D.③和④
下列四个选项中,属于全等图形的是()

点拨 根据全等图形的概念,能够完全重合的两个图形是全等图形可得答案。
解答:
解有所悟:一个图形经过平移、翻折、旋转后得到的新图形与原图形是全等图形。
A.①和②
B.②和③
C.①和③
D.③和④
答案:
A
典例2
如图,$\triangle ABF \cong \triangle CDE$,$\angle B和\angle D$是对应角,$AF和CE$是对应边。
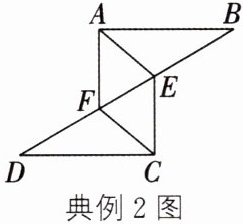
(1)写出$\triangle ABF和\triangle CDE$的其他对应角和对应边。
(2)若$\angle B = 30^{\circ}$,$\angle DCF = 40^{\circ}$,求$\angle EFC$的度数。
(3)若$BD = 10$,$EF = 2$,求$BF$的长。
点拨 (1)根据全等三角形的性质即可得出;(2)先根据全等三角形的性质求出$\angle D$的度数,再根据三角形内角和定理的推论即可求出;(3)根据全等三角形的性质,得$BF = DE$,求出$BE = DF = 4$,即可得到答案。
解答:
解有所悟:确定全等三角形对应边、对应角的方法:(1)字母顺序法:根据书写规范,按照对应顶点确定对应边、对应角。(2)图形特征法:① 最长边对应最长边,最短边对应最短边;② 最大角对应最大角,最小角对应最小角。(3)位置关系法:① 公共角或对顶角为对应角,公共边为对应边;② 对应角所对的边为对应边,两个对应角所夹的边为对应边;③ 对应边所对的角为对应角,两条对应边所夹的角为对应角。
如图,$\triangle ABF \cong \triangle CDE$,$\angle B和\angle D$是对应角,$AF和CE$是对应边。

(1)写出$\triangle ABF和\triangle CDE$的其他对应角和对应边。
(2)若$\angle B = 30^{\circ}$,$\angle DCF = 40^{\circ}$,求$\angle EFC$的度数。
(3)若$BD = 10$,$EF = 2$,求$BF$的长。
点拨 (1)根据全等三角形的性质即可得出;(2)先根据全等三角形的性质求出$\angle D$的度数,再根据三角形内角和定理的推论即可求出;(3)根据全等三角形的性质,得$BF = DE$,求出$BE = DF = 4$,即可得到答案。
解答:
解有所悟:确定全等三角形对应边、对应角的方法:(1)字母顺序法:根据书写规范,按照对应顶点确定对应边、对应角。(2)图形特征法:① 最长边对应最长边,最短边对应最短边;② 最大角对应最大角,最小角对应最小角。(3)位置关系法:① 公共角或对顶角为对应角,公共边为对应边;② 对应角所对的边为对应边,两个对应角所夹的边为对应边;③ 对应边所对的角为对应角,两条对应边所夹的角为对应角。
答案:
(1)其他对应角为∠BAF 和∠DCE,∠AFB 和∠CED;其他对应边为 AB 和 CD,BF 和 DE。(2)因为△ABF≌△CDE,∠B = 30°,所以∠B = ∠D = 30°。因为∠DCF = 40°,所以∠EFC = ∠D + ∠DCF = 30° + 40° = 70°。(3)因为△ABF≌△CDE,所以 BF = DE。所以 BF - EF = DE - EF。所以 BE = DF。因为 BD = 10,EF = 2,所以 BE = DF = 4。所以 BF = BE + EF = 4 + 2 = 6。
查看更多完整答案,请扫码查看


