《2025年暑期升级训练七年级数学浙教版浙江教育出版社》

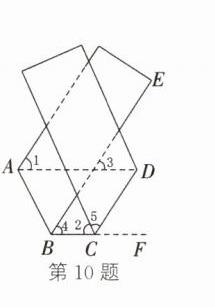
10. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为$AB$,$CD$. 若$CD// BE$,且$∠2 = 66^{\circ}$,则$∠1$的度数是()

A.$48^{\circ}$
B.$57^{\circ}$
C.$60^{\circ}$
D.$66^{\circ}$

答案：
B 解析:如图,延长 BC 至点 F. 因为纸带的对边互相平行,且 CD//BE,所以利用平行线的性质以及翻折的性质,可得∠5 = ∠DCF = ∠4 = ∠3 = ∠1. 因为∠2 + ∠5 + ∠DCF = 180°,所以 66° + 2∠5 = 180°. 所以∠5 = 57°. 所以∠1 = 57°.

11. 计算：$2025^{2} - 2024×2025 = $______.

答案： 2025

12. 已知$x ≠ y$,且满足两个等式$x^{2} - 2y = 2023^{2}$,$y^{2} - 2x = 2023^{2}$,则$x^{2} + 2xy + y^{2}$的值为______.

答案： 4 解析:联立 $\begin{cases}x^{2}-2y = 2023^{2}①, \\ y^{2}-2x = 2023^{2}②.\end{cases}$ 由① - ②,得 $x^{2}-y^{2}+2x - 2y = 0$. 所以 $(x + y)(x - y)+2(x - y)=0$,即 $(x - y)(x + y + 2)=0$. 由 $x ≠ y$,可得 $x + y + 2 = 0$,即 $x + y = -2$. 所以 $x^{2}+2xy + y^{2}=(x + y)^{2}=(-2)^{2}=4$.

13. 如图,两个完全一样的直角三角形有一部分重叠在一起,$AC与DE交于点O$. 若$AB = 10$,$DO = 4$,$BE = 6$,则涂色部分的面积为______.

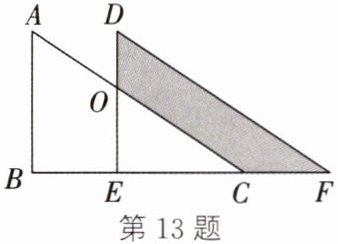
答案： 48

14. 已知关于$x$,$y的方程组\left\{\begin{array}{l} 2x - 3y = 3,\\ mx + ny = -1\end{array} \right.和\left\{unitable3 \right.$的解相同,则$(3m + n)^{2024}$的值为______.

答案： 1

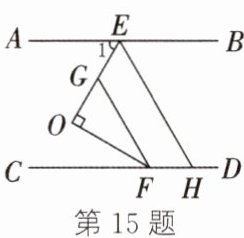
15. 如图,$AB// CD$,点$E$,$F分别在AB$,$CD$上,且$OE⊥OF$. 分别在$OE$,$CD上取点G$,$H$,使$FO平分∠CFG$. 要使$FG// EH$,那么$∠1与∠BEH$应满足的数量关系是______.

答案：
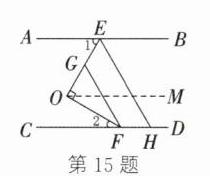
$∠1+\frac{1}{2}∠BEH = 90°$ 解析:如图,过点 O 作 OM//AB,所以∠1 = ∠EOM. 因为 AB//CD,所以 OM//CD. 所以∠2 = ∠FOM. 因为 OE⊥OF,所以∠EOF = 90°. 因为∠EOF = ∠EOM + ∠FOM,所以∠1 + ∠2 = 90°. 因为 AB//CD,所以∠BEH = ∠EHC. 因为 FG//EH,所以∠EHC = ∠CFG. 所以∠BEH = ∠CFG. 因为 FO 平分∠CFG,所以∠2 = $\frac{1}{2}∠CFG$. 所以∠2 = $\frac{1}{2}∠BEH$. 所以 $∠1+\frac{1}{2}∠BEH = 90°$.

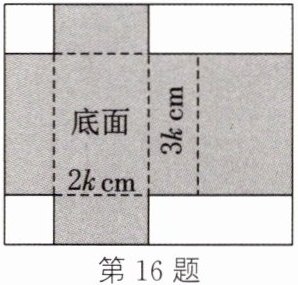
16. 如图,把一张长方形纸板裁去两个边长为 3cm 的小正方形和两个相同的小长方形,再把剩余部分(涂色部分)沿虚线折起,恰好可以折成一个有底有盖的长方体纸盒,纸盒底面长方形的长为$3kcm$,宽为$2kcm$.
(1)裁去的每个小长方形的面积为______$cm^{2}$(用含$k$的代数式表示).
(2)若长方体纸盒的侧面积是下底面积的正整数倍,则正整数$k$的值为______.

答案：
(1) $(6k + 9)$
(2) 1 或 5 解析:
(1) 由题意,得裁去的每个小长方形的长为 $(3 + 2k)$cm,宽为 3cm,所以裁去的每个小长方形的面积为 $(6k + 9)$cm².
(2) 设长方体纸盒的侧面积是下底面积的 n 倍(n 为正整数),则 $2(3×2k + 3×3k)=n·6k^{2}$. 所以 $nk = 5$. 因为 k 是正整数,所以 $n = 1,k = 5$ 或 $n = 5,k = 1$,即正整数 k 的值为 1 或 5.

17. (6 分)解方程(组)：
(1)(乐山中考)$\left\{\begin{array}{l} x - y = 1,\\ 3x + 2y = 8.\end{array} \right.$
(2)(山西中考)$\frac{1}{x - 1} + 1 = \frac{3}{2x - 2}$.

答案：
(1) $\begin{cases}x = 2, \\ y = 1.\end{cases}$
(2) $x=\frac{3}{2}$.

18. (5 分)(遂宁中考)先化简：$(1 - \frac{1}{x - 1})÷\frac{x - 2}{x^{2} - 2x + 1}$,再从 1,2,3 中选择一个合适的数作为$x$的值代入求值.

答案： $(1-\frac{1}{x - 1})÷\frac{x - 2}{x^{2}-2x + 1}=\frac{x - 1 - 1}{x - 1}÷\frac{x - 2}{(x - 1)^{2}}=\frac{x - 2}{x - 1}·\frac{(x - 1)^{2}}{x - 2}=x - 1$. 因为 $x - 1 ≠ 0,x - 2 ≠ 0$,所以 $x ≠ 1,x ≠ 2$. 当 $x = 3$ 时,原式 = 2.