第25页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
20.(6 分)在如图所示的网格图中,每个小正方形的边长均为 1,三角形 ABC 的三个顶点 A,B,C 都在格点(网格线的交点称为格点)上。现将三角形 ABC 平移,使点 A 平移到点 D,点 B,C 的对应点分别是 E,F。
(1)请在图中画出平移后的三角形 DEF。
(2)求三角形 DEF 的面积。
(3)在网格图中画出一个格点 P,使得$S_{三角形 BCP}= \frac{1}{2}S_{三角形 DEF}$(画出一个即可)。
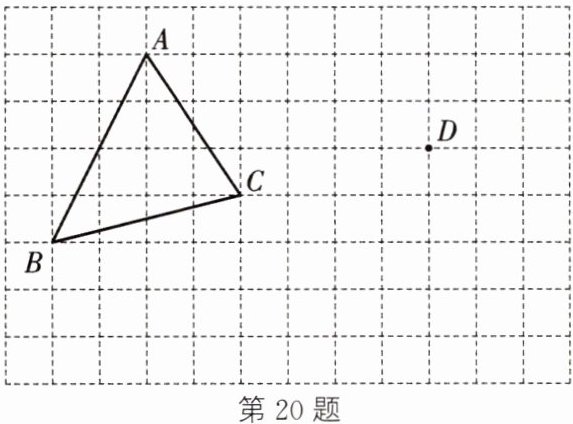
(1)请在图中画出平移后的三角形 DEF。
(2)求三角形 DEF 的面积。
(3)在网格图中画出一个格点 P,使得$S_{三角形 BCP}= \frac{1}{2}S_{三角形 DEF}$(画出一个即可)。

答案:
(1) 如图,三角形 DEF 即为所求.
(2) 三角形 DEF 的面积为 4×4 - $\frac{1}{2}$×2×3 - $\frac{1}{2}$×1×4 - $\frac{1}{2}$×2×4 = 7.
(3) 答案不唯一,如图,点 P 即为所求.

(1) 如图,三角形 DEF 即为所求.
(2) 三角形 DEF 的面积为 4×4 - $\frac{1}{2}$×2×3 - $\frac{1}{2}$×1×4 - $\frac{1}{2}$×2×4 = 7.
(3) 答案不唯一,如图,点 P 即为所求.

21.(8 分)水是生命之源,每一滴水都来之不易,让我们共同守护这份宝贵的资源,为未来创造更美好的生活。某校举行了水资源保护知识竞赛,为了解本次知识竞赛成绩情况,从参赛学生中随机抽取了若干名学生的初赛成绩进行统计,得到如下不完整的统计图表。
(1)求抽取的学生总人数和表中 a,b 的值。
(2)请补全频数直方图。
(3)将抽取的学生的竞赛成绩绘制成扇形统计图,若将成绩为$70≤x<90$的学生评为“良好”,求被评为“良好”的学生所在扇形圆心角的度数。
|成绩 x/分|频数|百分数|
|$60≤x<70$|15|10%|
|$70≤x<80$|a|20%|
|$80≤x<90$|60|40%|
|$90≤x≤100$|45|b|
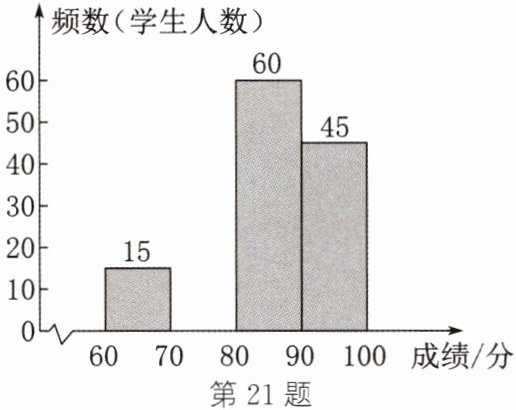
(1)求抽取的学生总人数和表中 a,b 的值。
(2)请补全频数直方图。
(3)将抽取的学生的竞赛成绩绘制成扇形统计图,若将成绩为$70≤x<90$的学生评为“良好”,求被评为“良好”的学生所在扇形圆心角的度数。
|成绩 x/分|频数|百分数|
|$60≤x<70$|15|10%|
|$70≤x<80$|a|20%|
|$80≤x<90$|60|40%|
|$90≤x≤100$|45|b|

答案:
(1) 抽取的学生总人数为 15 ÷ 10% = 150. a = 150×20% = 30,b = 45 ÷ 150×100% = 30%.
(2) 补全频数直方图如图所示.
(3) 被评为“良好”的学生所在扇形圆心角的度数为 360°×$\frac{30 + 60}{150}$ = 216°.

(1) 抽取的学生总人数为 15 ÷ 10% = 150. a = 150×20% = 30,b = 45 ÷ 150×100% = 30%.
(2) 补全频数直方图如图所示.
(3) 被评为“良好”的学生所在扇形圆心角的度数为 360°×$\frac{30 + 60}{150}$ = 216°.

查看更多完整答案,请扫码查看


