《2025年暑期升级训练七年级数学浙教版浙江教育出版社》

9. 如图,$\triangle ABD \cong \triangle CFD$,$AD \perp BC于点D$。延长$CF$,交$AB于点E$,连结$AC$。
(1)求证：$CE \perp AB$。
(2)若$BC = 7$,$AD = 5$,求$AF$的长。

答案： （1）因为 AD⊥BC，所以∠CDF = 90°。因为△ABD≌△CFD，所以∠BAD = ∠FCD。因为∠AFE = ∠CFD，所以∠AEF = ∠CDF = 90°。所以 CE⊥AB。（2）因为△ABD≌△CFD，所以 AD = CD，BD = FD。因为 BC = 7，AD = CD = 5，所以 BD = BC - CD = 2。所以 FD = 2。所以 AF = AD - FD = 5 - 2 = 3。

10. 如图,$\triangle ABC \cong \triangle ADE$,$BC的延长线交DE于点F$,$\angle D = 32^{\circ}$,$\angle E = 103^{\circ}$,$\angle DFB = 65^{\circ}$,则$\angle DAC = $____。

答案： 20°

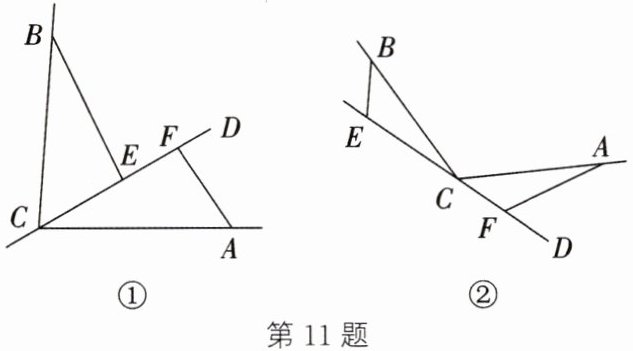
11. 已知$CD是经过\angle BCA的顶点C$的一条直线,$E$,$F是直线CD$上的两点,且$\triangle ACF \cong \triangle CBE$。
(1)如图①,当直线$CD经过\angle BCA$的内部时,请写出$EF$,$BE$,$AF$三条线段之间的数量关系,并给出证明。
(2)如图②,当直线$CD经过\angle BCA$的外部时,若$\angle BEC = 120^{\circ}$,求$\angle BCA$的度数。

答案： （1）EF + AF = BE。因为△ACF≌△CBE，所以 CF = BE，AF = CE。所以 EF + AF = EF + CE = CF = BE。（2）因为△ACF≌△CBE，所以∠ACF = ∠CBE。因为∠BCF = ∠BCA + ∠ACF = ∠BEC + ∠CBE，所以∠BCA = ∠BEC = 120°。