第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
1. 证明:要判断一个命题是真命题,往往需要从命题的____出发,根据已知的定义、____、____(包括____),一步一步推得结论成立。这样的推理过程叫作证明。
答案:
1. 条件 基本事实 定理 推论
2. 三角形的外角:由三角形的一条边的____和另一条相邻的边组成的角,叫作该三角形的外角。三角形的内角和定理的推论:三角形的外角等于与它____的两个内角的____。
答案:
2. 延长线 不相邻 和
3. 证明几何命题时,表述格式一般是:(1)按题意____。(2)分清命题的条件和结论,结合图形,在“____”中写出条件,在“____”中写出结论。(3)在“____”中写出推理过程。
答案:
3.
(1) 画出图形
(2) 已知 求证
(3) 证明
(1) 画出图形
(2) 已知 求证
(3) 证明
4. 解决几何问题时,有时需要添加辅助线。添加辅助线的过程要写入证明中。辅助线通常画成____。
答案:
4. 虚线
典例1 如图,BC//ED,BD平分∠ABC,EF平分∠AED。求证:BD//EF。
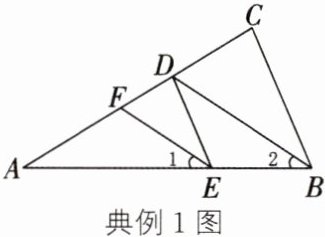
点拨 利用“三线八角”证出同位角相等后,即可证明BD//EF。
解答:
解有所悟:利用“三线八角”可使证明简洁明了。

点拨 利用“三线八角”证出同位角相等后,即可证明BD//EF。
解答:
解有所悟:利用“三线八角”可使证明简洁明了。
答案:
因为 BD 平分∠ABC,EF 平分∠AED(已知),所以∠2 = $\frac{1}{2}$∠ABC,∠1 = $\frac{1}{2}$∠AED(角平分线的定义)。因为 BC//ED(已知),所以∠ABC = ∠AED(两直线平行,同位角相等)。所以∠2 = ∠1(等量代换)。所以 BD//EF(同位角相等,两直线平行)。
典例2 求证:等腰三角形两腰上的高线长相等。
点拨 按证明几何命题的一般步骤证题,详见知识梳理3。如果第一步有困难,可先将原命题改写成“如果……那么……”的形式,便于理解。证题的思路是等面积法。
解答:
解有所悟:遇到高线或垂直时,利用等面积法建立等量关系。
点拨 按证明几何命题的一般步骤证题,详见知识梳理3。如果第一步有困难,可先将原命题改写成“如果……那么……”的形式,便于理解。证题的思路是等面积法。
解答:
解有所悟:遇到高线或垂直时,利用等面积法建立等量关系。
答案:
原命题改写为“如果两条线段是等腰三角形两腰上的高线,那么这两条线段相等”。已知:如图,在等腰三角形 ABC 中,AB = AC,BD,CE 分别是 AC,AB 边上的高线。求证:BD = CE。
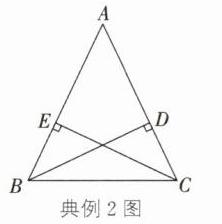
证明:因为在△ABC 中,BD,CE 分别是 AC,AB 边上的高线,所以 $ S_{△ABC} = \frac{1}{2}AC·BD = \frac{1}{2}AB·CE $。因为 AB = AC,所以 BD = CE。
原命题改写为“如果两条线段是等腰三角形两腰上的高线,那么这两条线段相等”。已知:如图,在等腰三角形 ABC 中,AB = AC,BD,CE 分别是 AC,AB 边上的高线。求证:BD = CE。

证明:因为在△ABC 中,BD,CE 分别是 AC,AB 边上的高线,所以 $ S_{△ABC} = \frac{1}{2}AC·BD = \frac{1}{2}AB·CE $。因为 AB = AC,所以 BD = CE。
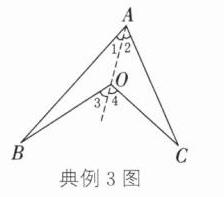
典例3 如图①所示的图形像我们常见的学习用品——圆规,我们不妨把这样的图形叫作“规形图”。
(1)如图①,观察“规形图”,试探究∠BOC与∠A,∠B,∠C之间的关系,并说明理由。
(2)如图②,在五角星中,利用(1)中的结论,求∠A+∠B+∠C+∠D+∠E的度数。

点拨 (1)连结AO并延长,为利用三角形内角或外角的性质创造条件。(2)利用(1)中的结论和对顶角相等,把5个角的和转化成三角形的内角和。
解答:
解有所悟:本题中的基本图形是“规形图”和“三角形”,复杂的图形是由基本图形构建成的。
(1)如图①,观察“规形图”,试探究∠BOC与∠A,∠B,∠C之间的关系,并说明理由。
(2)如图②,在五角星中,利用(1)中的结论,求∠A+∠B+∠C+∠D+∠E的度数。

点拨 (1)连结AO并延长,为利用三角形内角或外角的性质创造条件。(2)利用(1)中的结论和对顶角相等,把5个角的和转化成三角形的内角和。
解答:
解有所悟:本题中的基本图形是“规形图”和“三角形”,复杂的图形是由基本图形构建成的。
答案:
(1) ∠BOC = ∠BAC + ∠B + ∠C。理由:如图,连结 AO 并延长。因为∠3 是△ABO 的外角,所以∠1 + ∠B = ∠3①。因为∠4 是△AOC 的外角,所以∠2 + ∠C = ∠4②。由① + ②,得∠1 + ∠B + ∠2 + ∠C = ∠3 + ∠4,即∠BOC = ∠BAC + ∠B + ∠C。
(2) 由
(1)中的结论,可得∠A + ∠B + ∠E = ∠BFE。因为∠DFC = ∠BFE,所以∠A + ∠B + ∠E = ∠DFC。所以∠A + ∠B + ∠C + ∠D + ∠E = ∠DFC + ∠C + ∠D = 180°。
(1) ∠BOC = ∠BAC + ∠B + ∠C。理由:如图,连结 AO 并延长。因为∠3 是△ABO 的外角,所以∠1 + ∠B = ∠3①。因为∠4 是△AOC 的外角,所以∠2 + ∠C = ∠4②。由① + ②,得∠1 + ∠B + ∠2 + ∠C = ∠3 + ∠4,即∠BOC = ∠BAC + ∠B + ∠C。
(2) 由
(1)中的结论,可得∠A + ∠B + ∠E = ∠BFE。因为∠DFC = ∠BFE,所以∠A + ∠B + ∠E = ∠DFC。所以∠A + ∠B + ∠C + ∠D + ∠E = ∠DFC + ∠C + ∠D = 180°。

查看更多完整答案,请扫码查看


