第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
19. (5 分)试说明:多项式$(x^{2} - 4)(x^{2} - 10x + 21) + 100$的值一定是非负数.
答案:
原式 = $(x + 2)(x - 2)(x - 3)(x - 7)+100=(x + 2)(x - 7)(x - 2)(x - 3)+100=(x^{2}-5x - 14)(x^{2}-5x + 6)+100$. 设 $y = x^{2}-5x$,则原式 = $y^{2}-8y + 16=(y - 4)^{2}≥0$. 所以多项式 $(x^{2}-4)(x^{2}-10x + 21)+100$ 的值一定是非负数.
20. (7 分)解关于$x$,$y的方程组\left\{\begin{array}{l} mx + 2y = 6,\\ 2x + ny = 8\end{array} \right.$时,小军看错了方程组中的n,解得 .小红看错了方程组中的m,解得
.小红看错了方程组中的m,解得
.求:(1)$m$,$n$的值.
(2)该方程组正确的解.
 .小红看错了方程组中的m,解得
.小红看错了方程组中的m,解得
.求:(1)$m$,$n$的值.
(2)该方程组正确的解.
答案:
(1) 把 $\begin{cases}x=\frac{7}{3}, \\ y=\frac{2}{3}\end{cases}$ 代入第一个方程,得 $\frac{7}{3}m+\frac{4}{3}=6$,解得 $m = 2$. 把 $\begin{cases}x = -2, \\ y = 4\end{cases}$ 代入第二个方程,得 $-4 + 4n = 8$,解得 $n = 3$.
(2) 由
(1),得方程组为 $\begin{cases}2x + 2y = 6①, \\ 2x + 3y = 8②.\end{cases}$ 由② - ①,得 $y = 2$. 把 $y = 2$ 代入①,得 $2x + 4 = 6$,解得 $x = 1$. 所以该方程组正确的解为 $\begin{cases}x = 1, \\ y = 2.\end{cases}$
(1) 把 $\begin{cases}x=\frac{7}{3}, \\ y=\frac{2}{3}\end{cases}$ 代入第一个方程,得 $\frac{7}{3}m+\frac{4}{3}=6$,解得 $m = 2$. 把 $\begin{cases}x = -2, \\ y = 4\end{cases}$ 代入第二个方程,得 $-4 + 4n = 8$,解得 $n = 3$.
(2) 由
(1),得方程组为 $\begin{cases}2x + 2y = 6①, \\ 2x + 3y = 8②.\end{cases}$ 由② - ①,得 $y = 2$. 把 $y = 2$ 代入①,得 $2x + 4 = 6$,解得 $x = 1$. 所以该方程组正确的解为 $\begin{cases}x = 1, \\ y = 2.\end{cases}$
21. (9 分)新考法 探究题 (1)问题发现:如图①,直线$AB// CD$,$E为AB$,$CD$之间一点,连结$BE$,$CE$,可以发现$∠BEC = ∠B + ∠C$. 请把下面的过程补充完整:
解:如图①,过点$E作EF// AB$,
所以$∠B = ∠BEF$(______).
因为$AB// DC$,$EF// AB$,
所以$EF// DC$(______).
所以$∠C = ∠CEF$.
所以$∠B + ∠C = $______ + ______.
所以$∠BEC = ∠B + ∠C$(等量代换).
(2)探究:如果点$E$运动到如图②所示的位置,其他条件不变,试说明:$∠B + ∠C = 360^{\circ} - ∠BEC$.
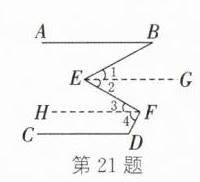
(3)解决问题:如图③,$AB// CD$,$E$,$F是AB与CD$之间的点,直接写出$∠B$,$∠BEF$,$∠EFD$,$∠D$之间的数量关系.

解:如图①,过点$E作EF// AB$,
所以$∠B = ∠BEF$(______).
因为$AB// DC$,$EF// AB$,
所以$EF// DC$(______).
所以$∠C = ∠CEF$.
所以$∠B + ∠C = $______ + ______.
所以$∠BEC = ∠B + ∠C$(等量代换).
(2)探究:如果点$E$运动到如图②所示的位置,其他条件不变,试说明:$∠B + ∠C = 360^{\circ} - ∠BEC$.
(3)解决问题:如图③,$AB// CD$,$E$,$F是AB与CD$之间的点,直接写出$∠B$,$∠BEF$,$∠EFD$,$∠D$之间的数量关系.

答案:
(1) 两直线平行,内错角相等;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;∠BEF;∠CEF.
(2) 过点 E 向左作 EF//AB. 因为 AB//CD,所以 AB//CD//EF. 所以∠B + ∠BEF = 180°,∠C + ∠CEF = 180°. 所以∠B + ∠BEF + ∠C + ∠CEF = 360°. 所以∠B + ∠C + ∠BEC = 360°. 所以∠B + ∠C = 360° - ∠BEC.
(3) 如图,过点 E 向右作 EG//AB,过点 F 向左作 FH//CD. 因为 AB//CD,所以 EG//AB//FH//CD. 所以∠4 + ∠D = 180°,∠B = ∠1,∠2 = ∠3. 所以∠1 + ∠2 = ∠B + ∠3. 所以∠BEF = ∠B + ∠3,即∠3 = ∠BEF - ∠B. 因为∠4 + ∠D = 180°,所以∠4 = 180° - ∠D. 所以∠3 + ∠4 = ∠BEF - ∠B + 180° - ∠D. 所以∠EFD = ∠BEF - ∠B + 180° - ∠D,即∠B + ∠D + ∠EFD - ∠BEF = 180°.
(1) 两直线平行,内错角相等;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;∠BEF;∠CEF.
(2) 过点 E 向左作 EF//AB. 因为 AB//CD,所以 AB//CD//EF. 所以∠B + ∠BEF = 180°,∠C + ∠CEF = 180°. 所以∠B + ∠BEF + ∠C + ∠CEF = 360°. 所以∠B + ∠C + ∠BEC = 360°. 所以∠B + ∠C = 360° - ∠BEC.
(3) 如图,过点 E 向右作 EG//AB,过点 F 向左作 FH//CD. 因为 AB//CD,所以 EG//AB//FH//CD. 所以∠4 + ∠D = 180°,∠B = ∠1,∠2 = ∠3. 所以∠1 + ∠2 = ∠B + ∠3. 所以∠BEF = ∠B + ∠3,即∠3 = ∠BEF - ∠B. 因为∠4 + ∠D = 180°,所以∠4 = 180° - ∠D. 所以∠3 + ∠4 = ∠BEF - ∠B + 180° - ∠D. 所以∠EFD = ∠BEF - ∠B + 180° - ∠D,即∠B + ∠D + ∠EFD - ∠BEF = 180°.

查看更多完整答案,请扫码查看


