《2025年暑期升级训练七年级数学浙教版浙江教育出版社》

9. 如图,在$\triangle ABC$中,$\angle ACB$是钝角. 若点$C在射线BD$上向右移动,则下列说法中,正确的是()


A.$\triangle ABC$先变成直角三角形,再变成锐角三角形,而不会再变成钝角三角形
B.$\triangle ABC$变成锐角三角形,而不会再变成钝角三角形
C.$\triangle ABC$先变成直角三角形,再变成锐角三角形,然后变成钝角三角形
D.$\triangle ABC$先变成直角三角形,再变成锐角三角形,接着变成直角三角形,然后变成钝角三角形

答案： D

10. 在如图所示的网格图中,有$A$,$B$,$C$,$D$,$E$五个点.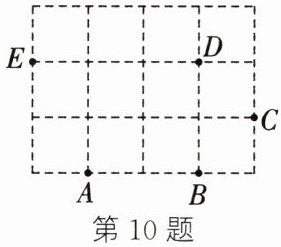
(1)以$AB$为一边,可以画出______个三角形.
(2)以$C$为顶点可以画出______个三角形.

答案：
(1) 3 解析：以AB为一边的三角形有△ABC，△ABD，△ABE，共3个.
(2) 6 解析：以C为顶点的三角形有△ABC，△BEC，△BCD，△ACE，△ACD，△CDE，共6个.

11. 若$a$,$b$,$c是\triangle ABC$的三边,则化简$\vert a - b - c\vert - \vert b + a - c\vert$的结果为______.

答案： 2c - 2a

12. 已知$a$,$b是\triangle ABC$的两条边的长,且满足$10a^{2} + 4b^{2} + 4 = 12ab + 4a$. 若该三角形的第三边的长$c$是奇数,求$c$的值.

答案： 因为10a² + 4b² + 4 = 12ab + 4a，所以10a² - 12ab + 4b² - 4a + 4 = 0. 所以9a² - 12ab + 4b² + a² - 4a + 4 = 0，即(3a - 2b)² + (a - 2)² = 0. 所以{3a - 2b = 0, a - 2 = 0,} 解得{a = 2, b = 3.} 所以3 - 2 ＜ c ＜ 3 + 2，即1 ＜ c ＜ 5. 又c是奇数，所以c = 3.

13. 三边长都是整数,且周长为$18$的三角形有几个？请分别写出这些三角形各边的长.

答案： 7个. 这些三角形各边的长如下：①8，8，2；②7，7，4；③6，6，6；④5，5，8；⑤3，7，8；⑥4，6，8；⑦5，6，7.