《2025年暑期升级训练七年级数学浙教版浙江教育出版社》

1. 基本事实：三边分别____的两个三角形全等(简写成“____”或“____”)。

答案： 1. 相等 边边边 SSS

2. 当三角形的三条边长确定时,三角形的形状、大小完全被确定,这个性质叫作三角形的____。

答案： 2. 稳定性

典例1 如图,盖房子时,在窗框没有安装之前,木工师傅常常先在窗框上斜钉一根木条,使其不变形,这种做法的根据是()
A. 两点之间线段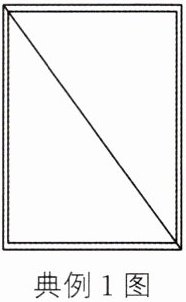最短
B. 长方形的对称性
C. 长方形四个角都是直角
D. 三角形的稳定性
点拨 理解窗框不变形的本质。
解答：
解有所悟：三角形的稳定性在实际生活中有着广泛的应用,如钢架桥、房屋架梁等,因此要使一些图形具有稳定的结构,往往通过添加线段将其转化为三角形而获得。

答案： D

典例2 如图,$AD= BC$,$BD= AC$。求证：$∠D= ∠C$。

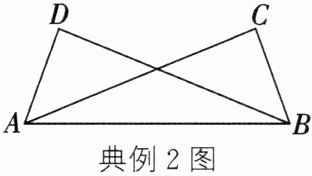
点拨 根据“SSS”推出$△ADB和△BCA$全等,再根据全等三角形的性质得出角相等。
解答：
解有所悟：在两个三角形中,如果已知两条边对应相等,那么可考虑证明第三条边也对应相等,从而利用“SSS”证明这两个三角形全等。找等边的方法：①中点；②公共边；③等线段加(或减)等线段,其和(或差)仍相等。

答案： 在$\triangle ADB$和$\triangle BCA$中，因为$\left\{\begin{array}{l} AD=BC,\\ BD=AC,\\ AB=BA,\end{array}\right. $所以$\triangle ADB\cong \triangle BCA(SSS)$。所以$∠D=∠C$。